こんにちは!個別指導WAMです(^^)/
今回は【グラフの平行移動】についてお話します。
この記事を読もうとしている方の中には、
「グラフの平行移動の公式を確認したい。」という方や
「正の方向に移動するのになぜマイナスが付くの?」
という疑問をもっている方もいらっしゃるのではないでしょうか。
この記事では、そういった疑問に答えていきます。
練習問題も用意していますので、
この機会にグラフの平行移動をマスターしましょう!
Contents [hide]
グラフの平行移動とは
【公式】グラフの平行移動
グラフの平行移動の公式は、以下の通りです。
<グラフの平行移動の公式>
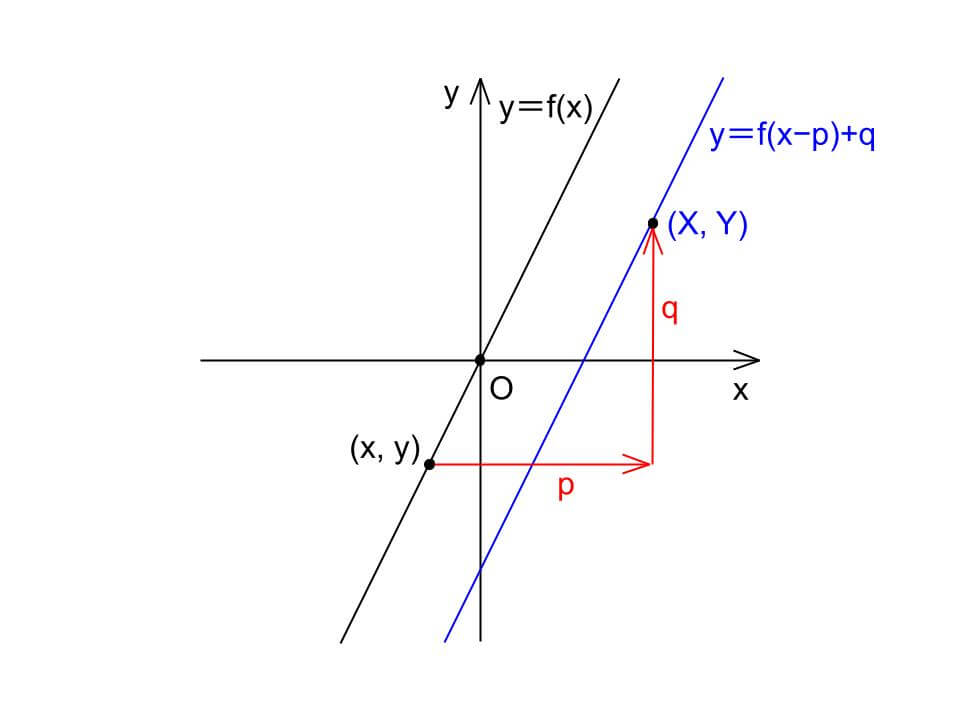
関数 y=f(x) のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動したグラフの方程式は、
「y−q=f(x−p)」
つまり
「y=f(x−p)+q」
どの関数のグラフや方程式においても、この公式が成り立ちます。
【解説】なぜマイナスになる?
公式から分かるように、グラフを x 軸方向に p 、y 軸方向に q だけ平行移動するときは、〈x を x−p〉 、〈y を y−q〉 に置き換えます。
ポイントは符号がマイナスになることです。
例えば、点の平行移動の場合は、点 (a, b) を x 軸方向に p 、y 軸方向に q だけ平行移動すると点 (a+p, b+q) になります。
しかし、グラフの平行移動の公式ではマイナスが付きます。それはなぜでしょうか?
公式の証明を通して考えてみましょう!
関数 y=f(x) のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動したとき、元のグラフ y=f(x) 上にある点 (x, y) は、点 (x+p, y+q) に移動しています。
この移動後の点を (X, Y)とすると、
X=x+p…①
Y=y+q…②
①、②より、
x=X−p…③
y=Y−q…④
③、④を y=f(x) に代入して、
Y−q=f(X−p)
よって、Y=f(X−p)+qとなり、グラフの平行移動の公式は成り立ちます。
公式の符号がマイナスになるのは、「移動後の座標から移動前の座標を見た」ときの関係性が式に表れるからなのです。
さまざまなグラフの平行移動
一次関数の平行移動の公式
一次関数 y=ax のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動したグラフの方程式は、
「y-q=a(x−p)」
つまり、
「y=a(x−p)+q」
二次関数の平行移動の公式
二次関数 y=ax² のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動したグラフの方程式は、
「y-q=a(x−p)²」
つまり、
「y=a(x−p)²+q」
二次関数 y=ax²+bx+c のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動したグラフは、
「y−q=a(x−p)²+b(x−p)+c」
つまり、
「y=a(x−p)²+b(x−p)+c+q」
三角関数の平行移動の公式
三角関数 y=a sin kθ のグラフを θ 軸方向に p 、y 軸方向に q だけ平行移動したグラフの方程式は、
「y=a sin k(θ−p)+q」
円の平行移動の公式
円 x²+y²=r² のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動したグラフの方程式は、
「(x−p)²+(y−q)²=r²」
グラフの平行移動の問題
一次関数の平行移動の問題
【問題】
y=3x のグラフを x 軸方向に 4 、y 軸方向に −8 だけ平行移動させたグラフの方程式を求めなさい。
また、そのグラフを描きなさい。
<解答>
y=3x のグラフを x 軸方向に 4 、y 軸方向に −8 だけ平行移動させたグラフの方程式は、
y=3(x−4)+(−8)
=3x−12−8
=3x−20
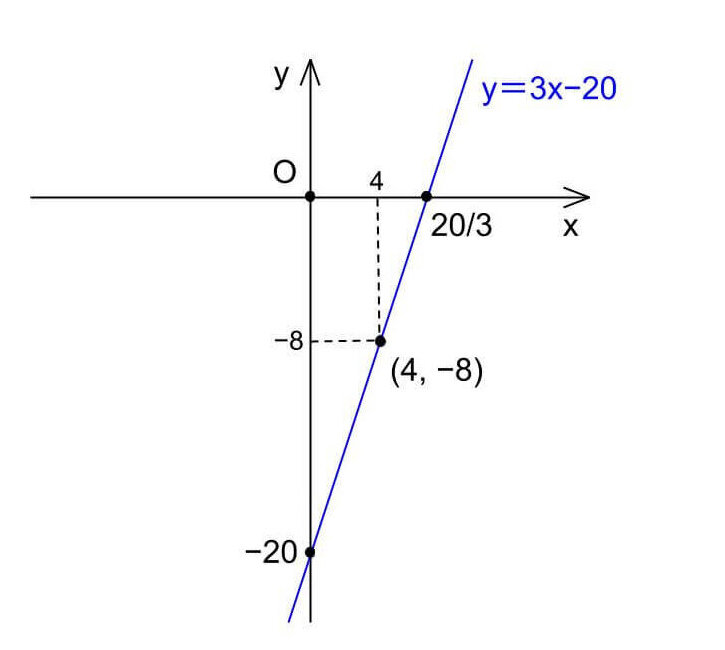
よって、y=3x−20
[x=0のとき、y=−20
y=0のとき、x=20/3
したがって、グラフは以下のようになる。]
二次関数の平行移動の問題
【問題】
y=1/2x²+3x+13/2 のグラフを x 軸方向に 9 、y 軸方向に −2 だけ平行移動させたグラフの方程式を求めなさい。
また、そのグラフを描きなさい。
<解答>
y=1/2x²+3x+13/2 のグラフを x 軸方向に 9 、y 軸方向に −2 だけ平行移動させたグラフの方程式は、
y=1/2(x−9)²+3(x−9)+13/2+(−2)
=1/2(x²−18x+81)+3x−27+9/2
=1/2x²−9x+81/2+3x−27+9/2
=1/2x²−6x+18
よって、y=1/2x²−6x+18
[y=1/2x²−6x+18
=1/2(x²−12x+36)
=1/2(x−6)²
よって、頂点は(6, 0)
x=0のとき、y=18
y=0のとき、x=6
したがって、グラフは以下のようになる。]
三角関数の平行移動の問題
【問題】
y=2 sin 2θ のグラフを θ 軸方向に π/2 、y 軸方向に 1 だけ平行移動させたグラフの方程式を求めなさい。
また、そのグラフを描きなさい。
<解答>
y=2 sin 2θ のグラフを θ 軸方向に π/2 、y 軸方向に 1 だけ平行移動させたグラフの方程式は、
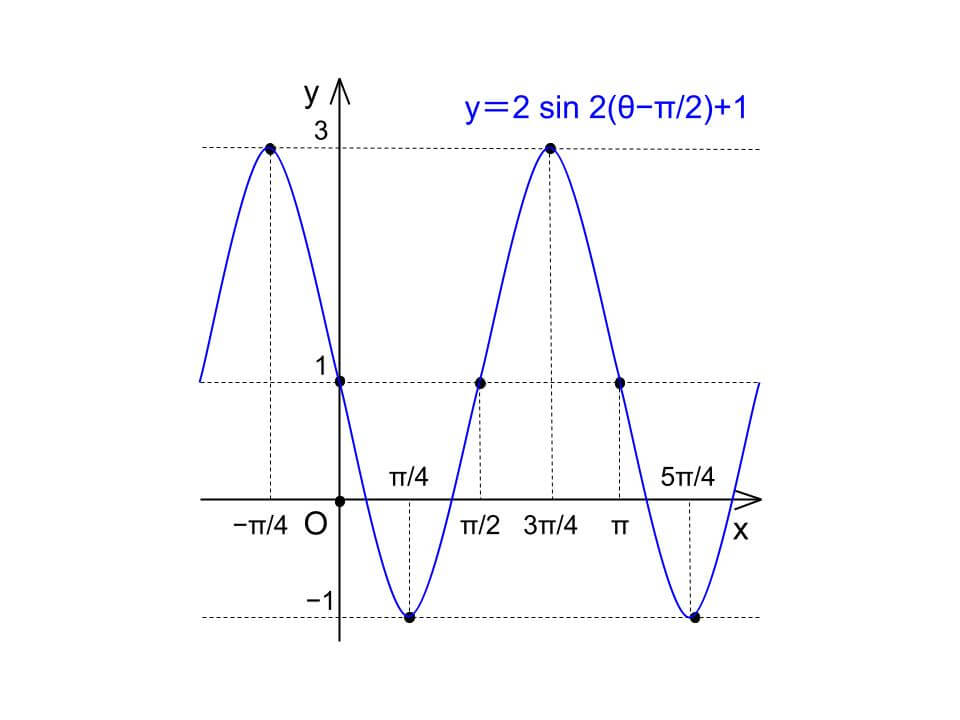
y=2 sin 2(θ−π/2)+1
[y=2 sin 2θ は y=sin θ のグラフを y 軸方向に 2 倍、θ 軸方向に 1/2 倍したものであり、それを θ 軸方向に π/2 、y 軸方向に 1 だけ平行移動させたグラフは、値域 −1 ≦ y ≦ 3 、周期 π で以下のようになる。]
円の平行移動の問題
【問題】
x²+y²=4² のグラフを x 軸方向に 8 、y 軸方向に 6 だけ平行移動させたグラフの方程式を求めなさい。
また、そのグラフを描きなさい。
<解答>
x²+y²=16 のグラフを x 軸方向に 8 、y 軸方向に 6 だけ平行移動させたグラフの方程式は、
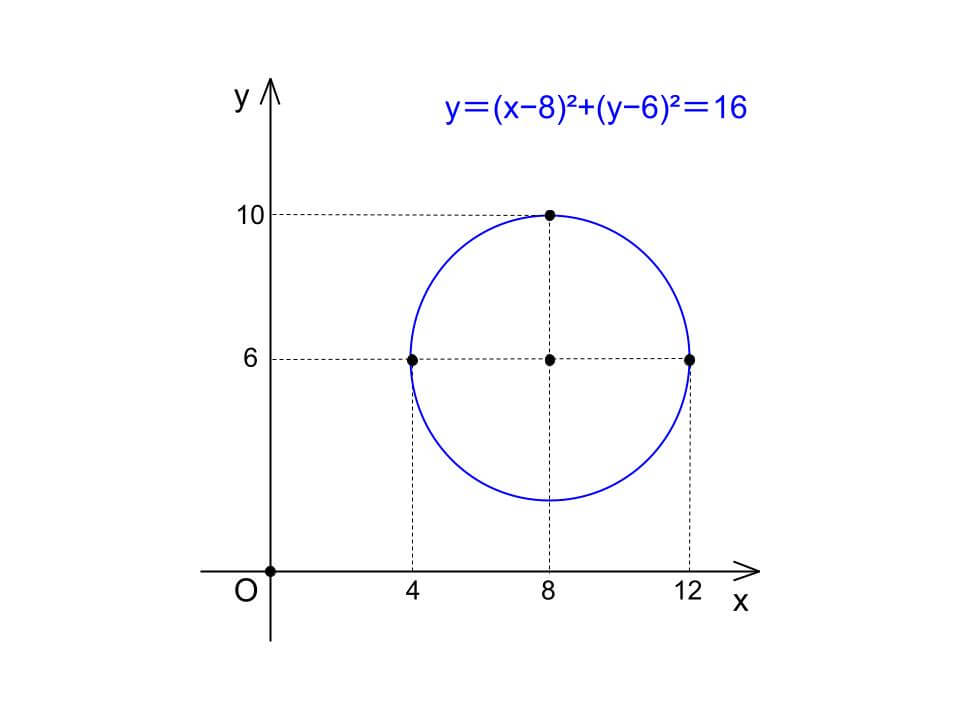
(x−8)²+(y−6)²=16
[したがって、円の中心は点 (8, 6) 、半径は 4 となり、グラフは以下のようになる。]
まとめ
グラフの平行移動についてご紹介してきましたが、いかがでしたか。
公式をしっかりと覚えて、グラフの平行移動をマスターしましょう!
さらにグラフの平行移動を理解するには、個別指導WAMがオススメです。
個別指導WAMでは、一人ひとりに合ったカリキュラムや学習アドバイスを通してきめ細かい指導を行っています。
ぜひお気軽にご相談ください。