こんにちは!個別指導WAMです(^^)/
図形はテストなどでよく出る単元ですが、苦手意識をお持ちの方は多いのではないでしょうか?
今回は、図形の単元から【平面図形の面積の求め方】についてお話したいと思います。
面積の中でも基本となりますので、表面積や体積が苦手という方はまずはここを押さえるようにしてくださいね。
Contents [hide]
平面図形の面積とは?
平面図形の面積は、小学校で習う内容で、立体ではない「三角形」や「四角形」「円」などの面積のことを指します。
次でそれぞれの図形の面積の求め方について、詳しく解説します。
面積の求め方
正方形・長方形
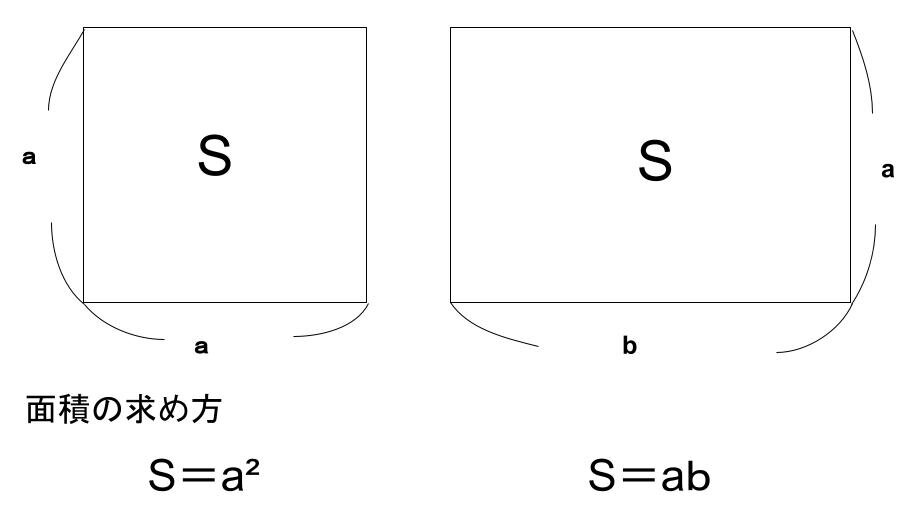
面積をS、縦の長さをa、横の長さをbとしたとき、
S=a×b(縦×横)
で求めることができます。
また正方形は一辺×一辺でも求めることができるので、S=a²でも求めることができます。
三角形
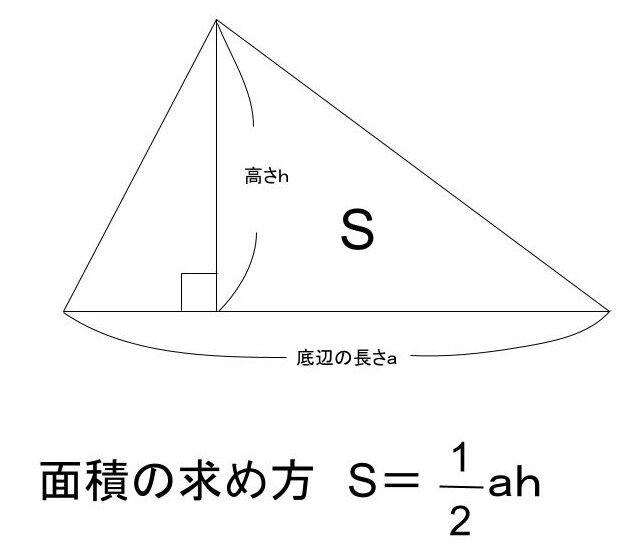
面積をS、底辺をa、高さをhとしたとき、
S=a×h÷2(底辺×高さ÷2)
で求めることができます。
平行四辺形
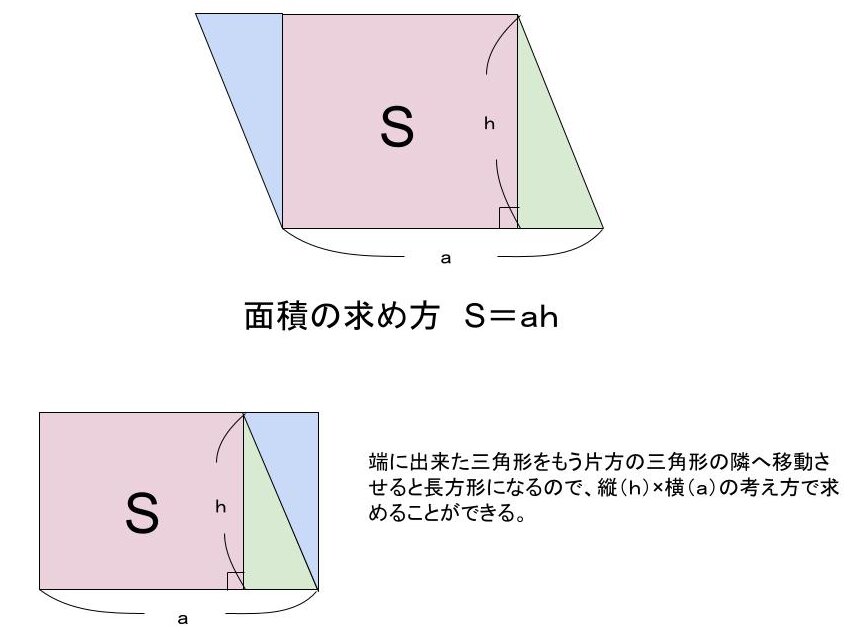
面積をS、底辺をa、高さをhとしたとき、
S=a×h(底辺×高さ)
で求めることができます。
ひし形
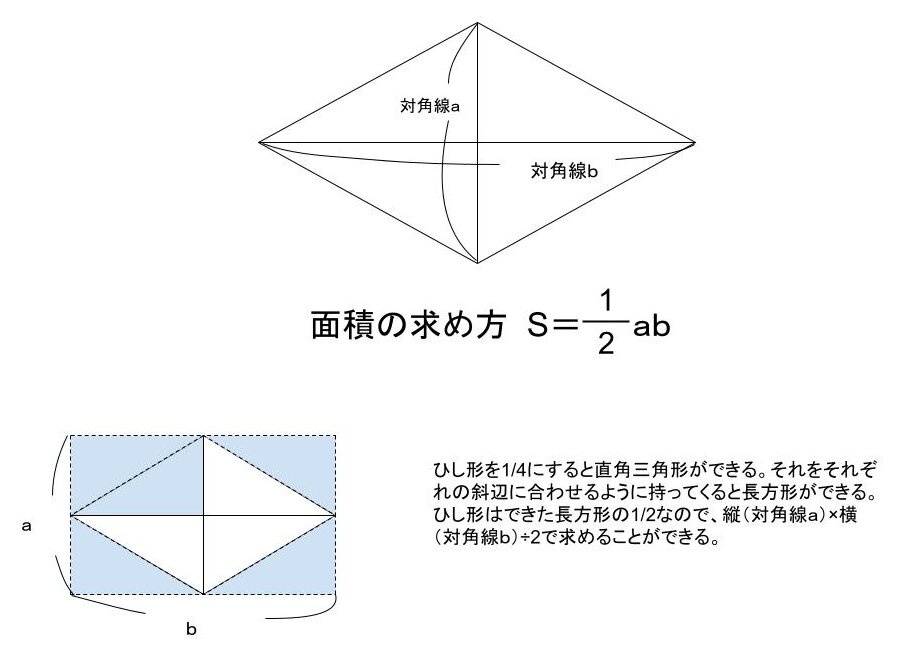
面積をS、対角線をそれぞれa・bとしたとき、
S=a×b÷2(対角線×対角線÷2)
で求めることができます。
台形
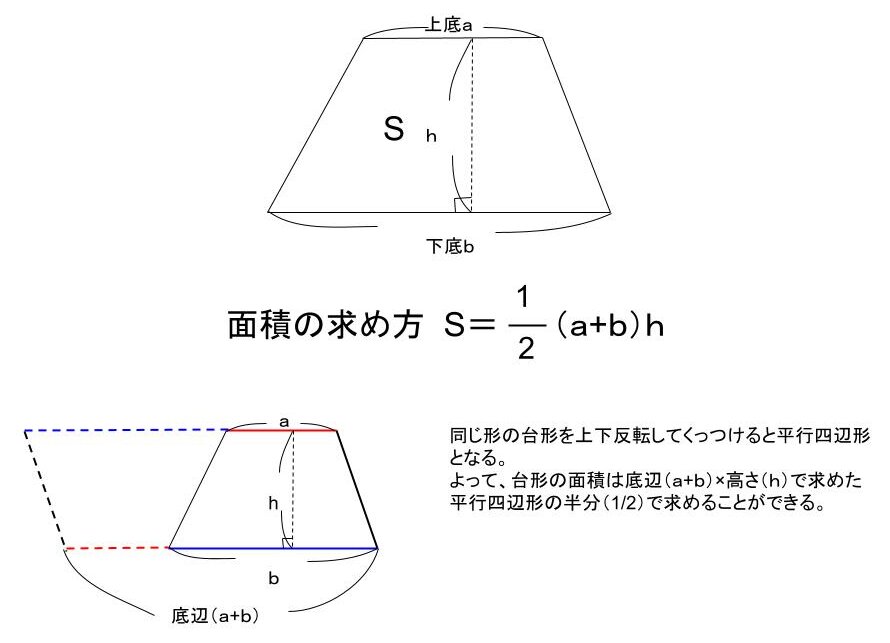
面積をS、上底をa、下底をb、高さをhとしたとき、
S=(a+b)×h÷2((上底+下底)×高さ÷2))
で求めることができます。
円
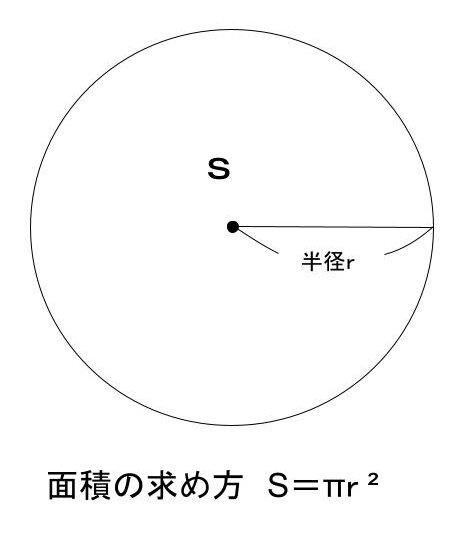
面積をS、半径をrとしたとき、
S=r×r× π(半径×半径×3.14)
で求めることができます。
扇形
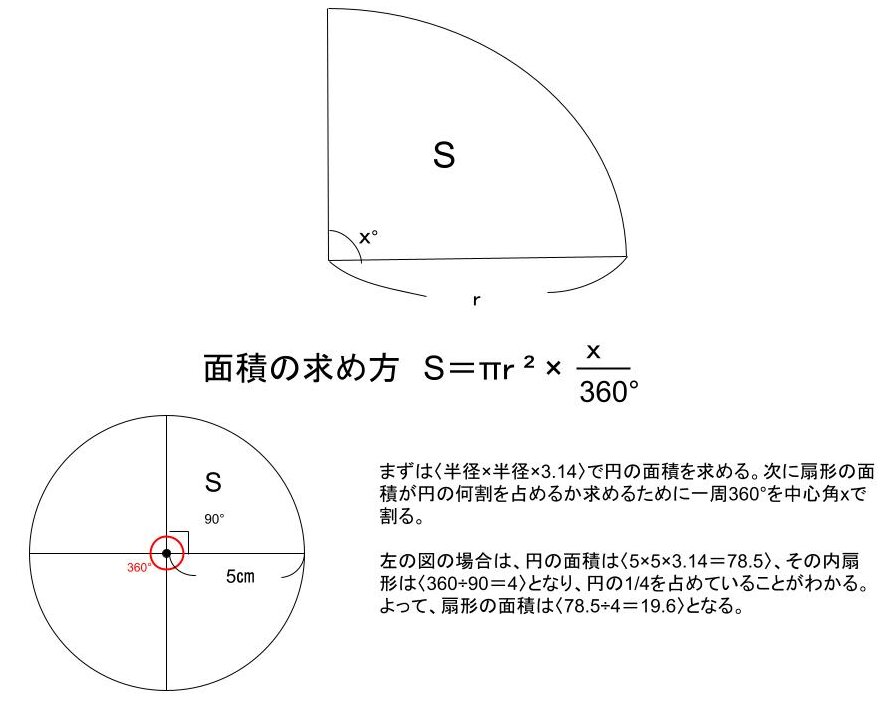
面積をS、半径をr、中心角をxとしたとき、
S=r×r×π×x°/360°(半径×半径×3.14×中心角/360°)
で求めることができます。
問題と解説
正方形
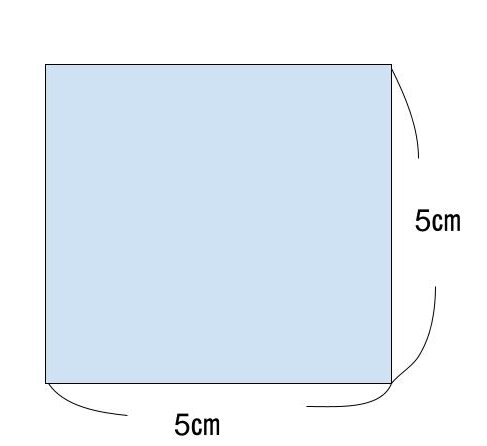
Q.一辺が5㎝の正方形の面積を求めよ
A.25㎠
【式】5×5=25
※正方形の面積の求め方:〈一辺×一辺〉
<h3長方形
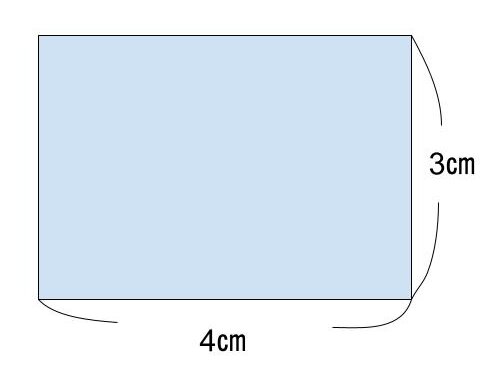
Q.縦3㎝、横4㎝の長方形の面積を求めよ
A.12㎠
【式】3×4=12
※長方形の面積の求め方:〈縦×横〉
三角形
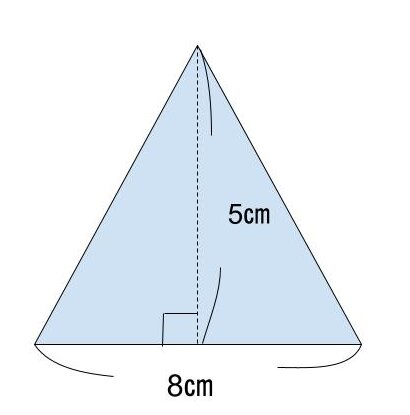
Q.底辺8㎝、高さ5㎝の三角形の面積を求めよ
A.20㎠
【式】8×5÷2=20
※三角形の面積の求め方:〈底辺×高さ÷2〉
平行四辺形
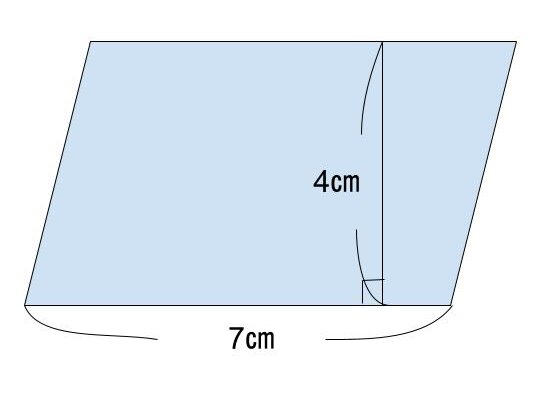
Q.底辺7㎝、高さ4㎝の平行四辺形の面積を求めよ
A.28㎠
【式】7×4=28
※平行四辺形の面積の求め方:〈底辺×高さ〉
ひし形
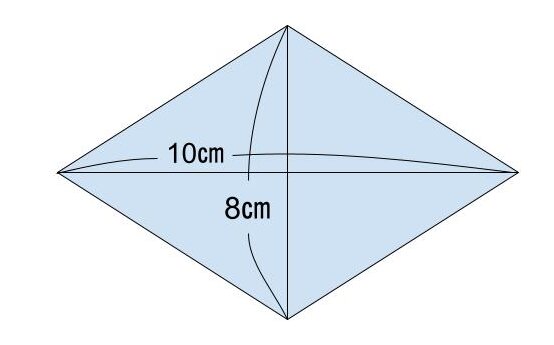
Q.対角線がそれぞれ10㎝、8㎝のひし形の面積を求めよ
A.40㎠
【式】10×8÷2=40
※ひし形の面積の求め方:〈対角線×対角線÷2〉
台形
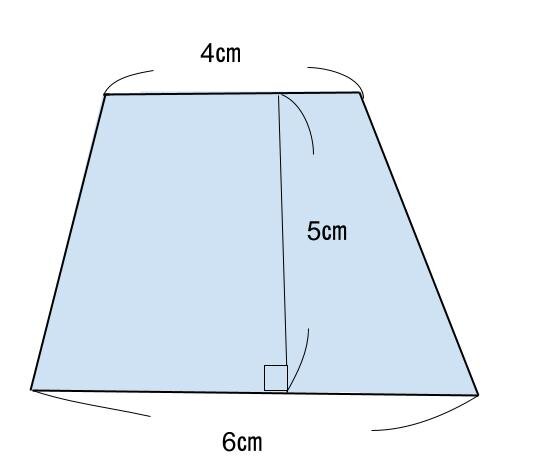
Q.上底が4㎝、下底6㎝、高さが5㎝の台形の面積を求めよ
A.25㎠
【式】(4+6)×5÷2=25
※台形の面積の求め方:〈(上底+下底)×高さ÷2〉
円
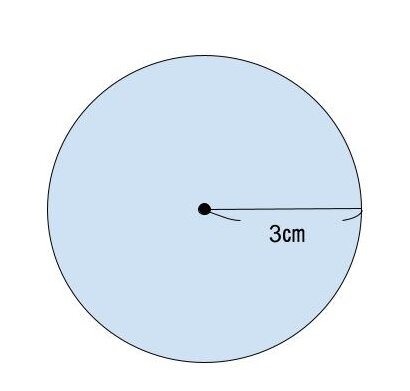
Q.半径3㎝の円の面積を求めよ
A.28.26㎠
【式】3×3×3.14=28.26
※円の面積の求め方:〈半径×半径×3.14〉
扇形
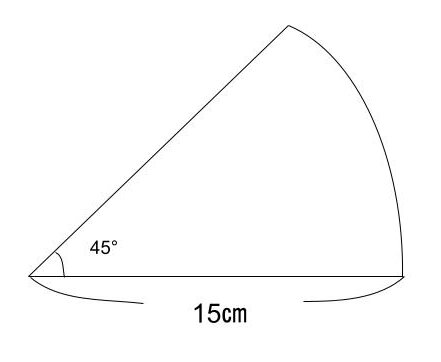
Q.半径15㎝、中心角が45°の扇形の面積を求めよ。(小数点第ニ位を四捨五入)
A.88.3㎠
【式】15×15×3.14×45/360=88.3
※扇型の面積の求め方:〈半径×半径×3.14×中心角/360〉
面積の求め方 一覧
最後に面積の求め方を整理してみます。
<正方形の面積の求め方>
「S=a²」(一辺×一辺)
<長方形の面積の求め方>
「S=ab」(縦×横)
<平行四辺形の面積の求め方>
「S=ah」(底辺×高さ)
<ひし形の面積の求め方>
「S=ab/2」(対角線×対角線÷2)
<台形の面積の求め方>
「S=h/2(a+b)」((上底+下底)×高さ÷2))
<円の面積の求め方>
「S=πr²」(半径×半径×3.14)
<扇形の面積の求め方>
「S=πr²× x/360」(半径×半径×3.14×中心角/360°)
繰り返しになりますが、平面積は様々な単元で使用されます。苦手意識を持たずしっかりと暗記してしまいましょう。
以下の記事でも平面積の公式を使用していますので、合わせて読んでみてください。
まとめ
いかがでしたか?
図と公式をセットで覚えて、面積をスムーズに導けるように何度も練習を行いましょう。
「一人では理解できたか不安…」「もっとたくさんの問題に触れたい」という方は是非一度個別指導WAMにご相談ください。
一人ひとりのニーズにあった学習方法をご提案し、丁寧に指導致します。













