こんにちは!個別指導WAMです(^^)/
今回は「不等式」について、その性質や解き方を解説したいと思います。
不等式といっても、絶対値の不等式や連立不等式、絶対値の不等式など様々な単元があります。
今回の記事では一次不等式を使用した基本の解説になりますので、
まずはここをしっかりと押さえるようにしてくださいね!
Contents [hide]
不等式とは
不等式とは、数の大小関係を示す「不等号」(>・<・≧・≦)を用い表した式のことです。
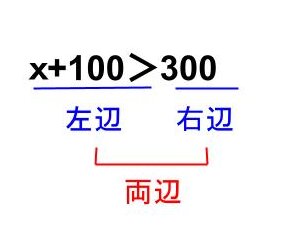
不等式の左側を左辺、右側を右辺といい、左辺と右辺を合わせて両辺といいます。
『左辺の項を右辺に移項する』といった言い方は、不等式だけでなく方程式などでもされています。
基本中の基本なので覚えておきましょう!
与えられた不等式の条件を満たすxの範囲を求めることを「不等式を解く」と言います。
文章問題などで式を立てる場合は、不等号の使い方にも注意するようにしましょう。
不等号の詳細については下記で詳しく解説していますので、参考にしてみてください。
不等式の基本性質
不等式を解くにあたり、不等式の4つの基本性質をしっかりと理解しておく必要があります。
特に気をつけなければならないのは、負の数をかけたり割ったりすると不等号の向きが変わる、ということです。
では、詳しく見てみましょう。
不等式の性質①
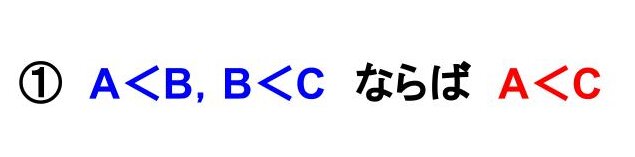
これは『AがBより小さく、BがCより小さいならば、AはCより小さい』という性質です。
つまり、『A<B<CなのでA<C』ということですね。
この性質のことを「不等式の推移律」といいます。
基本的なことなので、しっかりと理解しておきましょう。
不等式の性質②
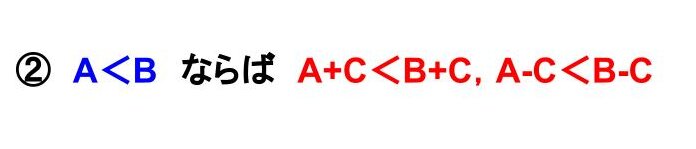
これは、『両辺に同じ数を足しても/両辺から同じ数を引いても、不等号の向きは変わらない』ことを示した性質です。
つまり、不等式の両辺には同じ数であれば足したり引いたりしてもいい、ということを指します。
この性質により、不等式を解く際に移項することが可能となります。
例
3x+2>20
3x>20-2
3x>18

不等式の性質③

これは、『Cが正の数であれば、両辺に同じ数を掛けても割っても、不等号の向きは変わらない』ことを示した性質です。
つまり、正の数であれば不等式の両辺に同じ数を掛けても割ってもいい、ということを指します。
例
5>3
という式の両辺に〈5〉を掛ける
25>15
大小関係は変わらない
不等式の性質④

これは、『Cが負の数の場合、両辺に同じ数を掛けたり割ったりすると、不等号の向きが変わる』ことを示した性質です。
例
5>3
という式の両辺に〈-5〉を掛ける
-25<-15
正負が逆転するので大小関係が変わる
この性質は不等式の単元において重要なポイントとなりますので、しっかりと覚えておきましょう。
問題と解説
不等式の性質について押さえたところで、実際に問題を解いてみましょう。
ここでは、不等式の基本となる一次不等式から出題したいと思います。
問題①
-6x>36
A.x<-6
【解説】
-6x>36・・・両辺を-6で割る
x<-6・・・不等式の性質④により不等号が逆転
★不等号があっているか確認したい場合はxに0などの数値を代入してみましょう。
・不等号を逆転しなかった場合
-6×0>36
0 >36
0が36より大きいことになるので間違い
・不等号を逆転した場合
-6×0<36
0<36
0は36より小さいので正しい
※この方法はほかの不等式でも使用できます。
問題②
3x+2<29
A.x<9
【解説】
3x+2<29
3x<29-2・・・2を移項する
3x<27・・・両辺を3で割る
x<9
問題③
x+4<3x-8
A. x > 6
【解説】
x+4<3x-8
x-3x<-8-4・・・左辺にx、右辺に数字となるよう移項する
-2x<-12・・・両辺を-2で割る
x>6・・・不等式の性質④により不等号が逆転
問題④
A君は母の日のプレゼントとして、1本150円のカスミソウを2本と1本200円のカーネーションをいくつか買うことにしました。A君の所持金が1,500円の時、カーネーションは最大で何本買うことができるでしょうか。
A.6本
【解説】
(150×2)+200x≦1500
200x≦1500-300
200x≦1200
x≦6
A君は最大で6本買うことができる
まとめ
いかがでしたか?
不等式の解き方は、基本的には方程式の解き方と同じです。
負の数の掛け算・割り算を行った時だけ不等号が逆転するということに注意して、丁寧に解くようにしましょう。
「一人では理解できたか不安…」「応用や連立不等式についても詳しく聞きたい」といった方は、是非一度個別指導WAMへご相談ください。
一人ひとりのお悩みにあった指導を行い、内容理解へのお手伝いをさせていただきます。













