こんにちは!個別指導WAMです(^^)
今回は、『表面積とは?立体図形ごとの求め方や練習問題を紹介!』についてご紹介します。
立体の表面積の求め方を知っていますか?
この記事を読もうとしている方の中には、
「表面積の公式は?」「表面積と体積はどう違う?」
という方もいらっしゃるのではないでしょうか。
この記事では、それらの疑問に答えていきます。下には練習問題も用意しています。
この機会に立体の表面積をマスターしましょう!
Contents [hide]
表面積とは
表面積と体積の違い
「表面積」とは、立体のすべての面の面積の和のことをいいます。外気に触れている面の面積の合計、水中に入れると濡れる部分の面積を足した値、とも言えます。単位は、「cm²(平方センチメートル)」「m²(平方メートル)」「a(アール)」「ha(ヘクタール)」などになります。
「体積」とは、立体の嵩(かさ)のことをいいます。その立体が占める場所の大きさのことで、中身が詰まっているもののボリューム、とも言えます。単位は、「cm³(立方センチメートル)」「m³(立方メートル)」「ml(ミリリットル)」「l(リットル)」などになります。
立体ごとの表面積の求め方
立方体
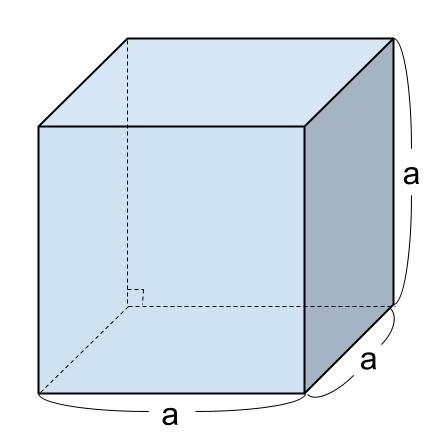
立方体の表面積を S 、一辺の長さを a とするとき、立方体の表面積は
S = a × a × 6( 一辺 × 一辺 × 面の数 )
= 6a²
で求めることができます。
<立方体の表面積の求め方>
「 S = 6a² 」
直方体
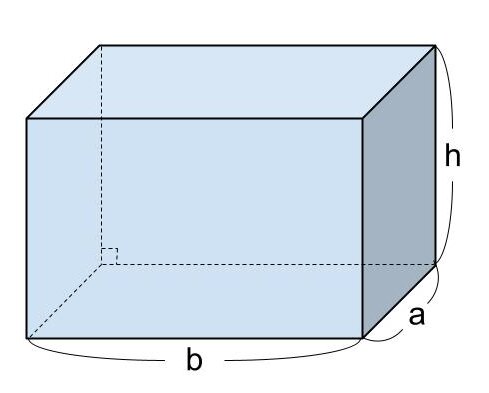
直方体の表面積を S 、底面の縦の長さを a 、横の長さを b 、高さを h とするとき、直方体の表面積は
S = a × b × 2 + a × h × 2 + b × h × 2( 縦 × 横 × 2 + 縦 × 高 さ × 2 + 横 × 高さ × 2 )
=2( ab + ah + bh )
で求めることができます。
<直方体の表面積の求め方>
「 S = 2( ab + ah + bh )」
角柱
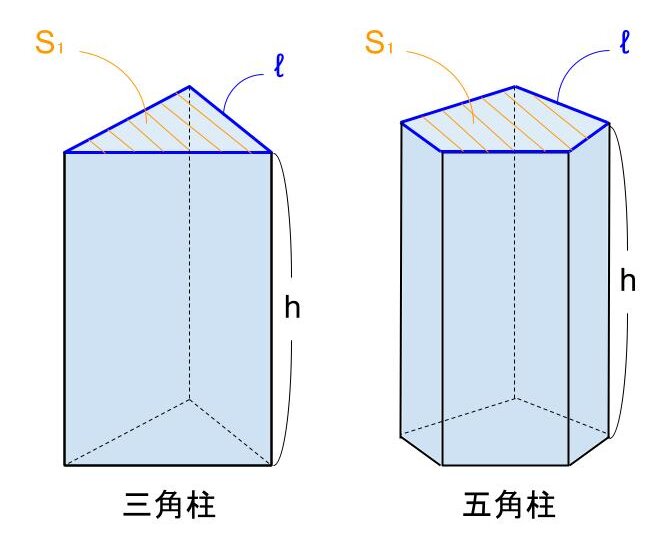
角柱の表面積を S 、底面の辺の長さの合計を ℓ 、高さを h とするとき、角柱の表面積は
S = ( 低面積 ) × 2 + ℓ × h
=2( 低面積 ) + ℓh
で求めることができます。
<角柱の表面積の求め方>
「 S = 2( 低面積 ) + ℓh 」
円柱
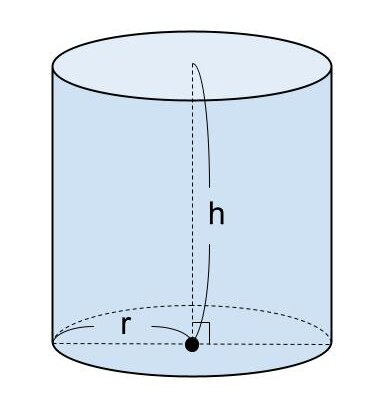
円柱の表面積を S 、底面の半径を r 、高さを h 、円周率を π とするとき、円柱の表面積は
S = r × r × π × 2 + r × 2 × π × h( 低面積 × 2 + 円周の長さ × 高さ )
= 2πr² + 2πrh
= 2πr ( r + h )
で求めることができます。
<円柱の表面積の求め方>
「 S = 2πr ( r + h ) 」
角錐
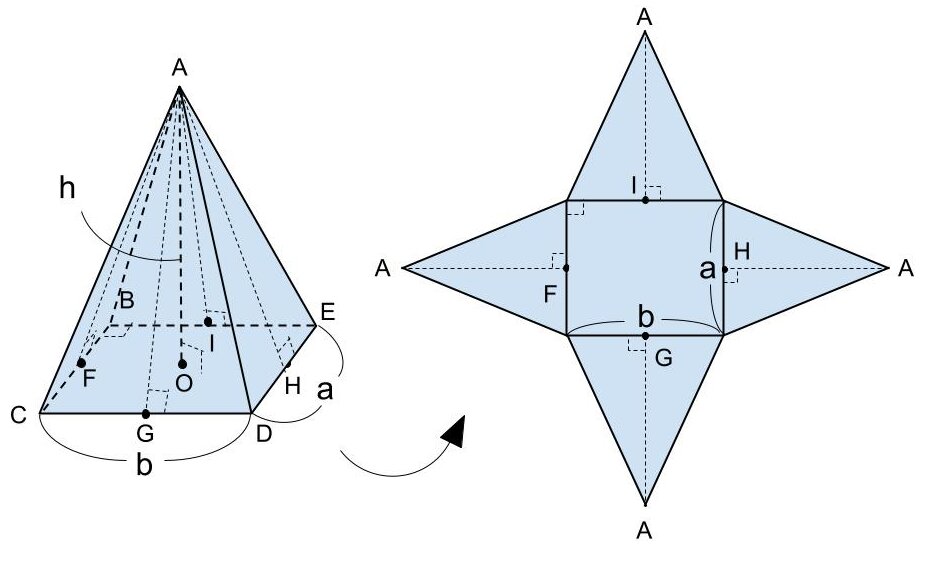
角錐の表面積を S 、低面積の縦の長さを a 、横の長さを b とするとき、角錐の表面積はS=(低面積)+(側面積)で求めることができます。
例えば図のような底面が長方形の四角柱の場合、
AG = AI
= √h² + ( a / 2 )²
AH = AF
= √h² + ( b / 2 )²
S = a × b + 1/2 × ( √h² + ( b / 2 )²) × a × 2 + 1/2 × ( √h² + ( a / 2 )²) × b × 2
= ab + a ( √h² + ( b / 2 )²) + b ( √h² + ( a / 2 )²)
<角錐の表面積の求め方>
「S = ( 低面積 ) + ( 側面積 ) 」※底面の形によって異なる
円錐

円錐の表面積を S 、底面の半径を r 、高さを h 、母線の長さをℓ、円周率をπとするとき、円錐の表面積は
S = r × r × π + ℓ × ℓ × π × ( r × 2 × π / ℓ × 2 × π )( 低面積 + 母線を半径とする円の面積 × 母線を半径とする円の円周の長さ ÷ 底面の円周の長さ )
= πr² + πrℓ
= πr² + πr√r² + h²
で求めることができます。
<円錐の表面積の求め方>
「S = πr² + πrℓ
= πr² + πr√r² + h² 」
球
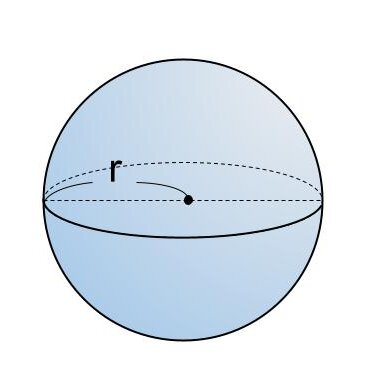
球の表面積を S 、半径を r 、円周率を π とするとき、球の表面積は
S = r × r × π × 4
= 4πr²
で求めることができます。
<球の表面積の求め方>
「 S = 4πr² 」
表面積の問題
立方体の問題
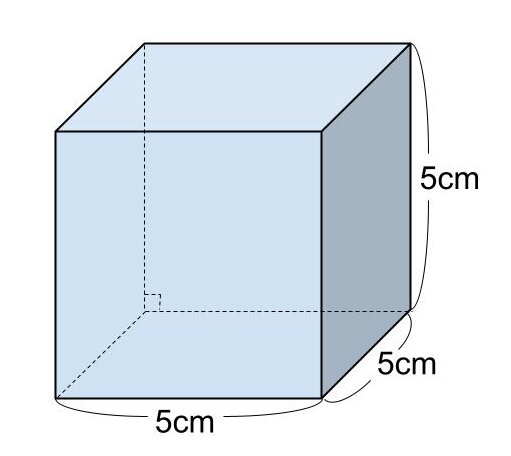
【問題】一辺が5cmの立方体の表面積を求めなさい。
<解答>
立方体の表面積を S とする。
S = 6 × 5²
= 150
よって、立方体の表面積は150cm²
直方体の問題
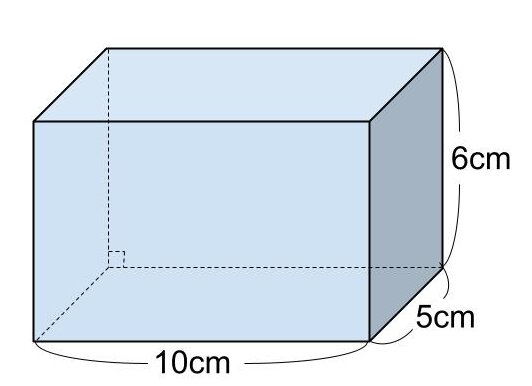
【問題】
底面の縦の長さが5cm、横の長さが10cm、高さが6cmの直方体の表面積を求めなさい。
<解答>
直方体の表面積を S とする。
S = 2 ( 5 × 10 + 5 × 6 + 10 × 6 )
= 20 ( 5 + 3 + 6 )
= 20 × 14
= 280
よって、直方体の表面積は280cm²
角柱の問題
【問題】
図のような三角柱と五角柱の表面積を求めなさい。
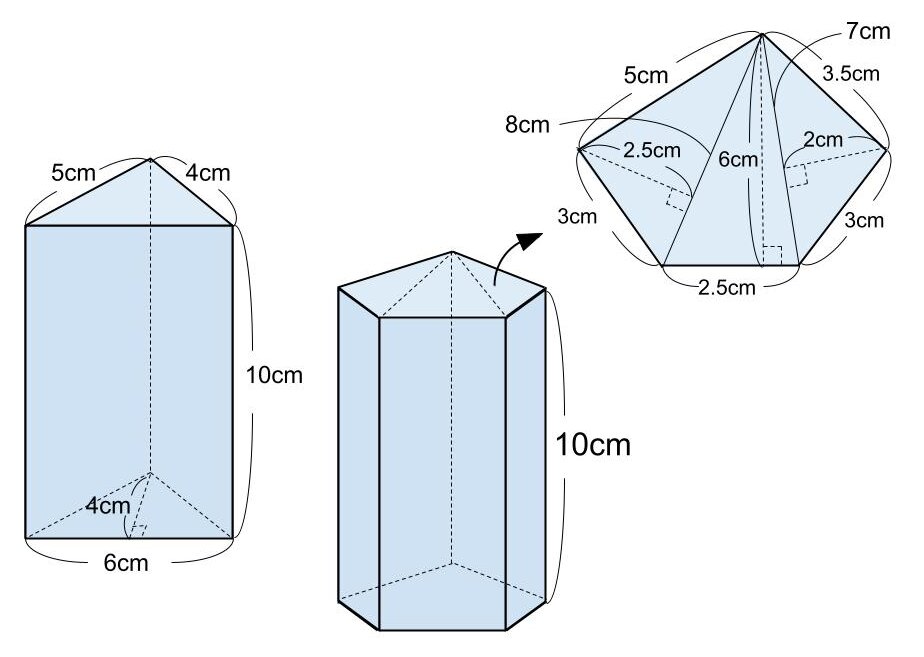
<解答>
三角柱の表面積をS₁、五角柱の表面積をS₂とする。
S₁ = 1/2 × 4 × 6 × 2 + ( 5 + 6 + 4 ) × 10
= 24 + 150
= 174
S₂ = ( 1/2 × 2.5 × 8 + 1/2 × 6 × 2.5 + 1/2 × 2 × 7 ) × 2 + ( 5 + 3 + 2.5 + 3 + 3.5 ) × 10
= 2 {( 10 + 7.5 + 7 ) + 17 × 5 }
= 2 × 109.5
= 219
よって、三角柱の表面積は174cm²、五角柱の表面積は219cm²
円柱の問題
【問題】
円周率を π とするとき、底面の半径が4cm、高さが8cmの円柱の表面積を求めなさい。
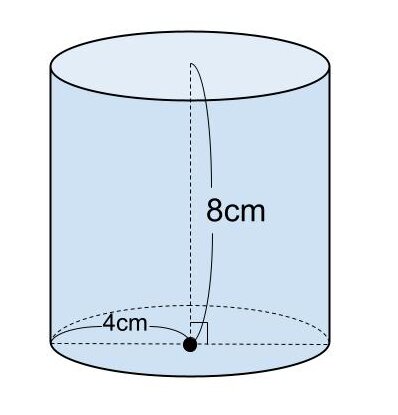
<解答>
円柱の表面積を S とする。
S = 2π × 4 ( 4 + 8 )
= 96π
よって、円柱の表面積は96πcm²
角錐の問題
【問題】
図のような四角柱の表面積を求めなさい。
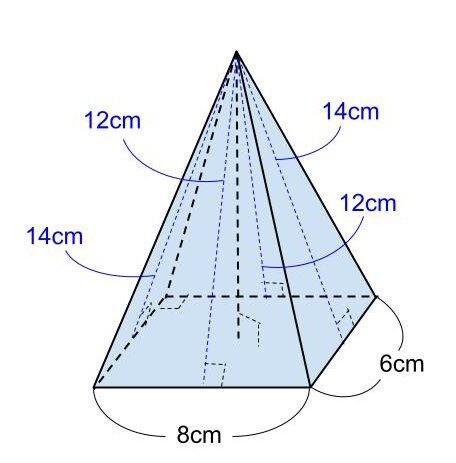
<解答>
四角柱の表面積を S とする。
S = 6 × 8 + 1/2 × 12 × 8 × 2 + 1/2 × 14 × 6 × 2
= 12 × ( 4 + 8 + 7 )
= 12 × 19
= 228
よって、四角柱の表面積は228cm²
円錐の問題
【問題】
円周率をπとするとき、半径が3cm、高さが4cmの円錐の表面積を求めなさい。
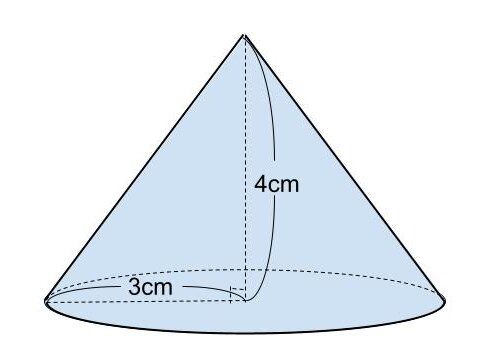
<解答>
円錐の表面積を S とする。
S = π × 3² + π × 3√3² + 4²
= 4²π + 3√25π
= ( 16 + 15 ) π
= 31π
よって、円錐の表面積は31πcm²
球の問題
【問題】
円周率をπとするとき、半径7cmの球の表面積を求めなさい。
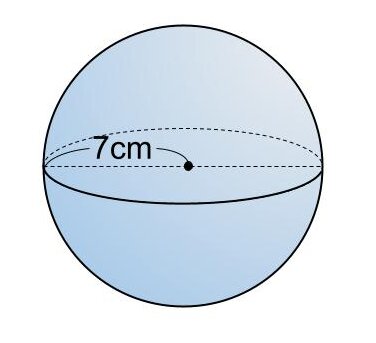
<解答>
球の表面積を S とする。
S = 4π × 7²
= 196π
よって、球の表面積は196πcm²
表面積の求め方まとめ
・立方体の表面積の求め方
「 S = 6a² 」
・直方体の表面積の求め方
「 S = 2 ( ab + ah + bh )」
・角柱の表面積の求め方
「 S = 2 ( 低面積 ) + ℓh 」
・円柱の表面積の求め方
「 S = 2πr ( r + h )」
・角錐の表面積の求め方
「 S = ( 低面積 ) + ( 側面積 )」※底面の形によって異なる
・円錐の表面積の求め方
「 S = πr² + πrℓ
= πr² + πr√r² + h² 」
・球の表面積の求め方
「 S = 4πr² 」
まとめ
いかがでしたか。
表面積の意味や求め方についてご紹介しました。
表面積は「 低面積 + 側面積 」が基本形ですが、底面の数や形によって求め方は異なります。立体ごとの求め方を覚えて、立体の表面積をマスターしましょう。
さらに表面積の求め方を理解するには、個別指導WAMがオススメです。
個別指導WAMは、一人ひとりに合ったカリキュラムや学習アドバイスを通してきめ細かい指導を行っています。
ぜひお気軽にご相談ください!













