こんにちは!個別指導WAMです(^^)
今回は、『底面積とは?【○○柱】【○○錐】の底面積の求め方』についてご紹介します。
図形問題はテストによく出る単元ですが、立体について苦手意識を持っている方は多いのではないでしょうか?
今回の記事では、《立体の底面の面積=底面積》についてお話します。
底面積を求め方を覚えることができれば、立体の体積を求める公式も簡単に覚えることができますよ!
底面積とは?
「底面積」とは、立体の底面の面積のことを指します。
立体には円柱や三角錐など様々な形があり、底面積の求め方は底面の形によって異なります。
「底面積」という文字を見ると新たな公式が出てくるように感じる方もいるかもしれませんが、底面積の求め方は、平面で習う面積の求め方と同じです。
次で詳しく解説します。
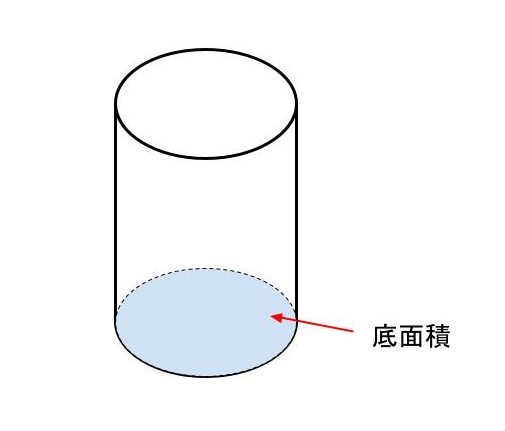
底面積の求め方
底面積の前に、立体の種類を2つ確認したいと思います。
1つめは「○○柱」と呼ばれるもので、上と下の底面が全く同じ形をしていて太さが一定のものを指します。
2つめは「○○錐」と呼ばれるもので、上にいくにしたがい細くなり、頂点が尖っているものを指します。
○○の部分にはそれぞれ底面の形の名称が入ります。
例えば、底面が四角形の○○柱であれば「四角柱」、底面が円の○○錐であれば「円錐」となります。
底面が四角の場合
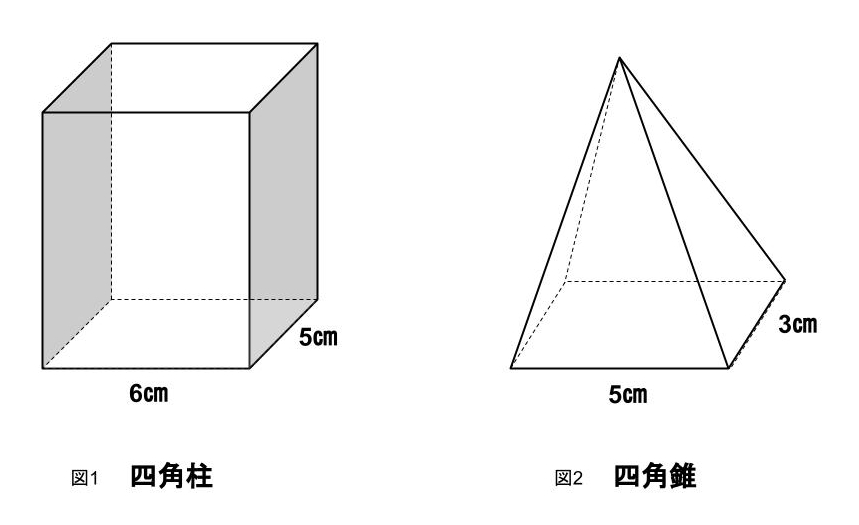
底面が四角形の立体は「四角柱」と「四角錐」となります。
これらの底面積は、四角形の面積の求め方で求めることができるので【縦×横】となります。
図1 四角柱
5×6=30 A.30㎠
図2 四角錐
3×5=15 A.15㎠
底面が三角の場合
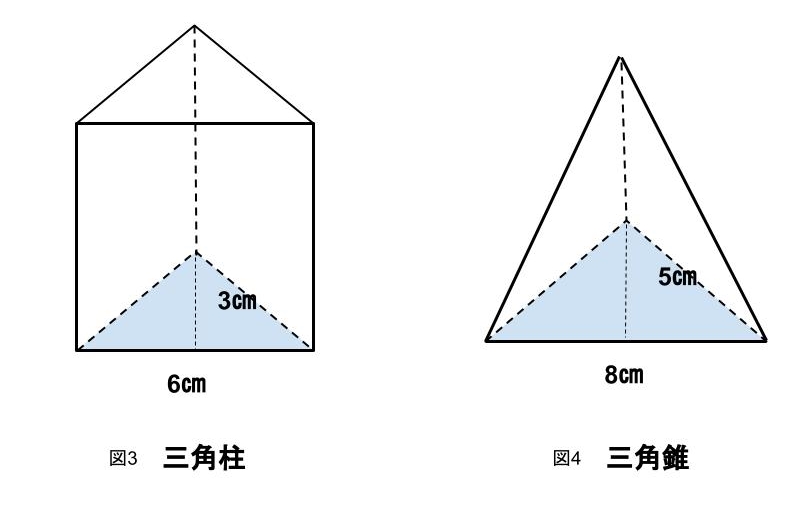
底面が三角形の立体は「三角柱」と「三角錐」となります。
これらの底面積は、三角形の面積の求め方で求めることができるので【底辺×高さ÷2】となります。
図3 三角柱
6×3÷2=9 A.9㎠
図4 三角錐
8×5÷2=20 A.20㎠
底面が円の場合
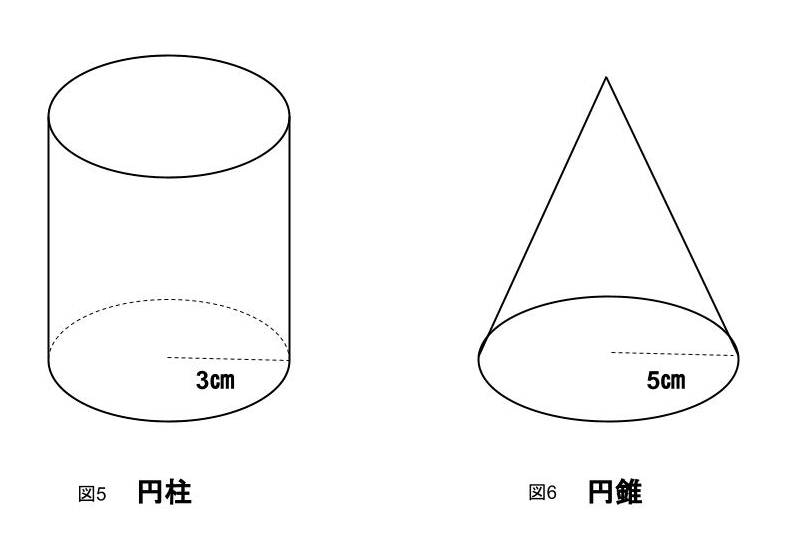
底面が円の立体は「円柱」と「円錐」となります。
これらの底面積は、円の面積の求め方で求めることができるので【半径×半径×3.14】となります。
図5 円柱
3×3×3.14=28.26 A.28.26㎠
図6 円錐
5×5×3.14=78.5 A.78.5㎠
底面が台形の場合
底面が台形の立体は四角形の時と同様に「四角柱」と「四角錐」と呼ばれます。
ですが、底面が四角形ではないので【縦×横】では求められません。
この場合は、台形の面積の求め方となりますので【 (上底+下底)×高さ÷2】となります。
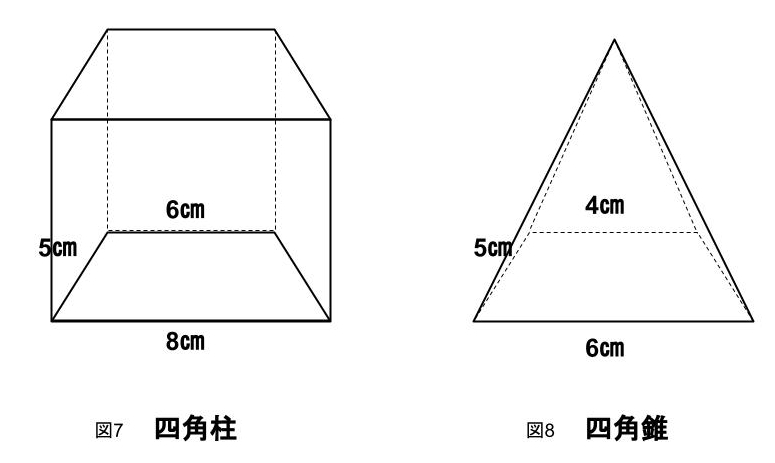
図7 四角柱
(8+6)×5÷2=35 A.35㎠
図8 四角錐
(6+4)×5÷2=25 A.25㎠
体積の求め方
底面積を求めることができれば、「○○柱」と「○○錐」の体積を簡単に求めることができます。
それぞれの立体の体積の求め方は以下の通りです。
●四角柱・・・【縦×横×高さ】
●三角柱・・・【底辺×(底面の)高さ÷2×(三角柱の)高さ】
●円柱・・・【半径×半径×3.14×高さ】
●四角錐・・・【縦×横×高さ÷3】
●三角錐・・・【底辺×(底面の)高さ÷2×(三角柱の)高さ÷3】
●円錐・・【半径×半径×3.14×高さ÷3】
どうでしょうか。
「こんなの覚えられない…」と思った方も諦めないでください!
気づいた方もいるかもしれませんが、実はこれ「○○柱」は【底面積×高さ】、「○○錐」は【底面積×高さ÷3】になっているんです。
つまり底面積の求め方を覚えることができれば、あとは【×高さ】か【×高さ÷3】なのかを覚えればいいだけです。
沢山の公式を覚えることが苦手な方もそう考えれば覚えられる気がしませんか?
もう少し詳しく体積について知りたい方は以下の記事も参考にしてみてください。
まとめ
いかがでしたか?
底面積は一見難しそうですが、平面図形の面積の求め方と同じです。
しっかりと覚えて立体の問題に取り組むようにしましょう!
「ひとりでは理解できたか心配」「もっと立体について勉強してみたい」といった方は是非一度、個別指導WAMへご相談ください。
一人ひとりにあった学習方法をご提案し、不安解消や内容理解へ向けたサポートをいたします。













