こんにちは!個別指導WAMです(^^)/
今回は三角形の一種である「直角三角形」についての定義や、テストによくでてくる形について解説していきます。
直角三角形のポイントを押さえることができれば、関連する問題に素早く対応できるようになります。
Contents [hide]
直角三角形とは
直角三角形とは
直角三角形とは「三角形の3つの角の内、1つの角が直角である三角形」のことを指します。
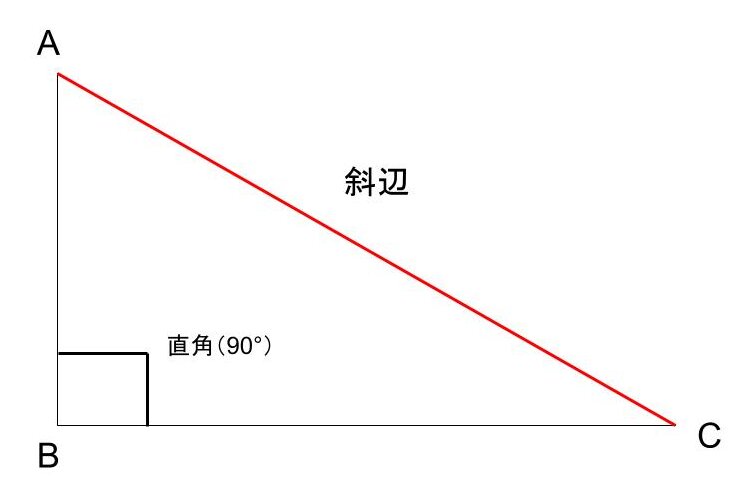
直角以外の角は90°以下の鋭角となり、直角の対辺を斜辺と言います。斜辺は直角三角形の中で最も長い辺となります。
三平方の定理(ピタゴラスの定理)
三平方の定理
三平方の定理とは「斜辺以外の二辺の長さの二乗の和は、斜辺の二乗に等しい」という公式になります。
下記のような三角形がある場合、
【a²+b²=c²】
で表されます。
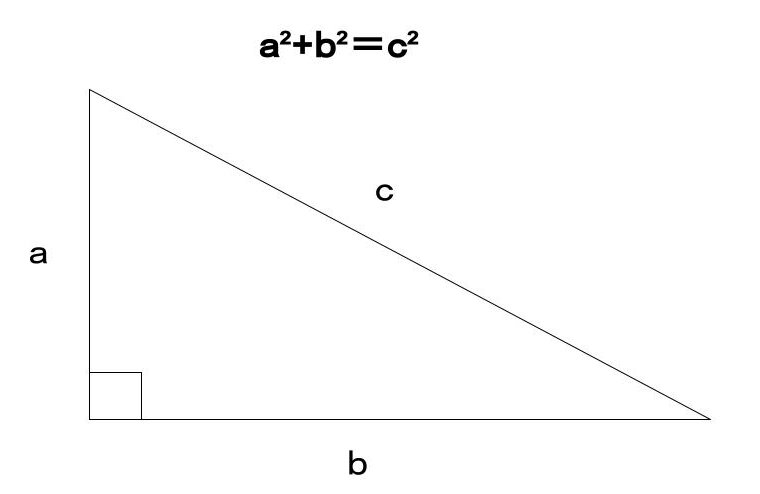
三平方の定理を覚えておけば、2辺の長さがわかっている時に残りの1辺の長さを求めることができます。
ピタゴラス数
三平方の定理が成り立つ整数の組み合わせのことをピタゴラス数と呼びます。
有名な組み合わせとして【3:4:5】という比があります。テストにもよく出てきますので暗記しておきましょう。
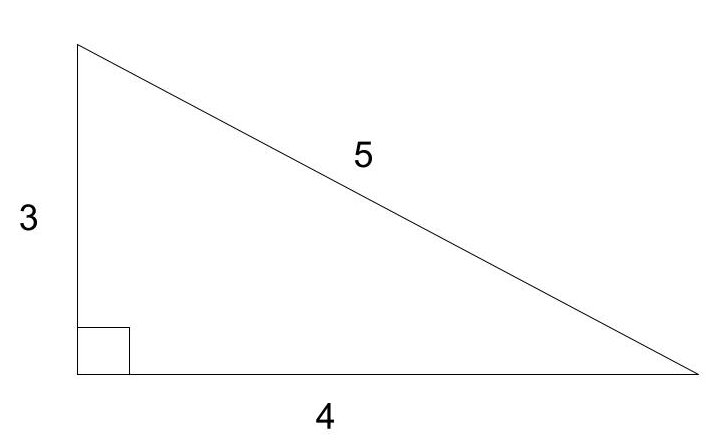
【3:4:5】以外にも、【5:12:13】や【8:15:17】などもピタゴラス数として有名なので覚えておくといいでしょう。
覚えておくと便利な直角三角形
直角三角形の中にはテストなどでよく使われる有名なものがあります。
その内3つを紹介しますので、ぜひ覚えてください。
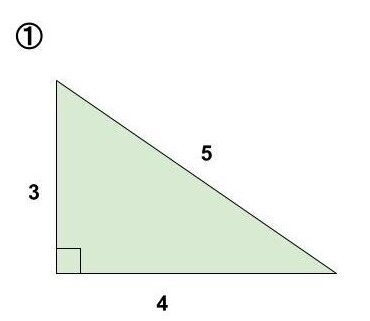
図①
ピタゴラス数でもお話した【3:4:5】の比になっている三角形です。
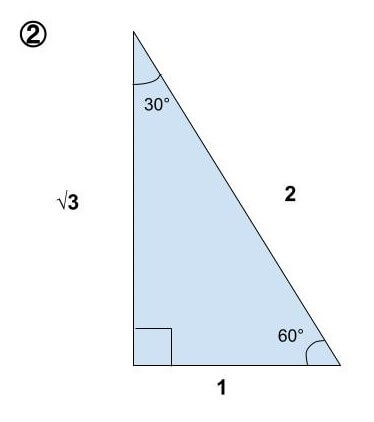
図②
角度が【30°】【60°】【90°】となっている三角形です。正三角形を半分に切ったときにあらわれる直角三角形となります。三辺の比は【1:2:√3】です。
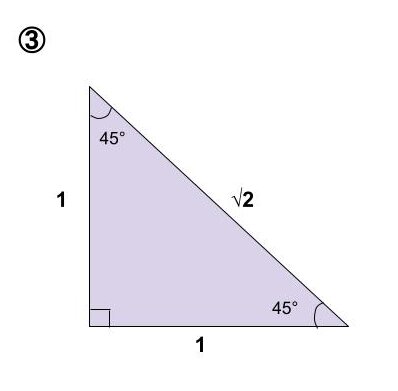
図③
直角二等辺三角形です。角度が【45°】【45°】【90°】、3辺の比が【1:1:√2】となります。
直角三角形の合同条件
1つの角度が90°と決まっている直角三角形の合同条件は次の2つです。
①斜辺と 1 つの鋭角がそれぞれ等しい
②斜辺と他の 1 辺がそれぞれ等しい
共通しているのは〈斜辺の長さがそれぞれ等しい〉ということですね。では詳しく見てみましょう。
①斜辺と 1 つの鋭角がそれぞれ等しい
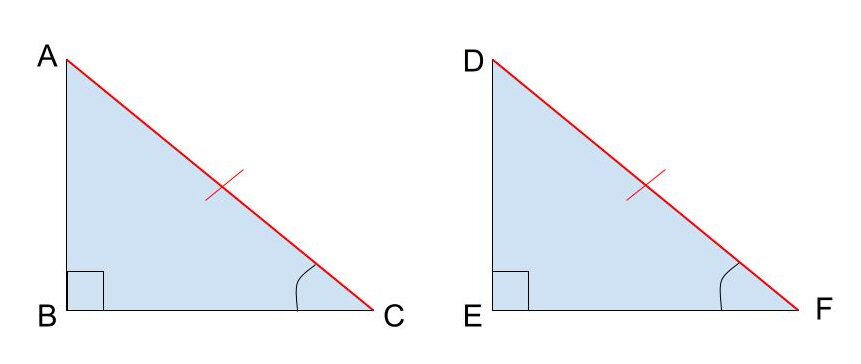
図のように
∠ABD=∠DEF=90°
AC=DF(斜辺)
∠ACB=∠DFE
である三角形の場合、〈①斜辺と 1 つの鋭角がそれぞれ等しい〉を満たしているので△ABC≡△DEFが証明できます。
直角三角形の場合、1つの角は必ず90°なので、2つの鋭角の内、1つの角度がわかっていれなおのずと残りの1つの鋭角の角度も求めることができるます。よって、三角形の合同条件である「1組の辺とその両端の角がそれぞれ等しい」を満たすことができます。
②斜辺と他の 1 辺がそれぞれ等しい
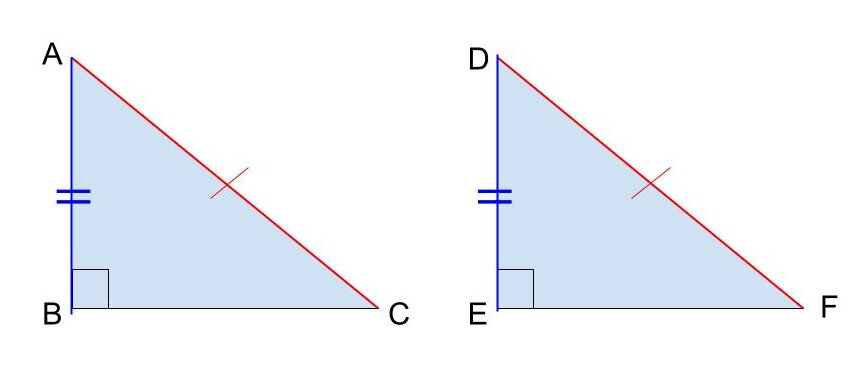
図のように
∠ABD=∠DEF=90°
AC=DF(斜辺)
AB=DF
である三角形の場合、〈②斜辺と他の 1 辺がそれぞれ等しい〉を満たしているので△ABC≡△DEFが証明できます。
斜辺は直角に向かい合う辺と決まっているので、他の1辺の長さが等しければ残りの辺の長さも等しいと言えます。よって、三角形の合同条件である「3組の辺がそれぞれ等しい」を満たすことができます。
まとめ
いかがでしたか?
三角形の中でも直角三角形は特殊な形であり、定理や独自の合同条件が存在します。しっかりと覚えて、問題に対応できるようになりましょう。
「もっと図形について知りたい」「一人ではわからない」という方は是非一度個別指導WAMへご相談ください。
ひとりひとりの理解度に合わせた丁寧な指導を行います。













