こんにちは!個別指導WAMです(^^)
立体の体積の求め方を知っていますか?
今回は、立体ごとの体積の求め方についてお話します!
この機会に立体の体積をマスターしましょう!
Contents [hide]
立体の種類
立方体
「立方体」とは、6つの合同な正方形だけで囲まれた立体のことをいいます。正多面体のひとつであり、正六面体ともいいます。
8つの「頂点」、12本の「辺」、6つの「面」からなります。それぞれの頂点には3つの平面が集まり、すべての辺が同じ長さで、向かい合う面は平行になっており、隣り合う面は直角に交わります。
サイコロ、ルービックキューブ、角砂糖などに立方体が用いられています。
直方体
「直方体」とは、6つの長方形(正方形を含む)だけで囲まれた立体のことをいいます。四角柱のひとつであり、六面体ともいいます。
8つの「頂点」、12本の「辺」、6つの「面」からなります。それぞれの頂点には3つの平面が集まり、向かい合う面はすべて平行になっており、隣り合う面は直角に交わります。すべての面が正方形であるものを特に「立方体」といいます。
直方体は、お菓子のパッケージや消しゴム、建造物などに見ることができます。
角柱
「角柱」とは、2つの合同かつ平行な多角形と、その間の四角形で構成される立体のことをいいます。
角柱の向かい合う2つの合同かつ平行な多角形を「底面」、周りの面を「側面」といい、2つの底面の距離が「高さ」です。柱体のうち、底面が多角形になっているものを角柱といいます。底面が三角形であれば三角柱、四角形であれば四角柱です。
菱餅や将棋の駒、新品の鉛筆などが角柱となっています。
円柱
「円柱」とは、2つの平行な円について、“2つの円の中心を結んだ直線に平行で、かつ2つの円の円周に交わる線分” が描く曲面と、2つの円が囲む立体のことです。
円柱の向かい合う2つの円を「底面」、周りの曲面を「側面」といい、2つの底面の距離が「高さ」です。柱体のうち、底面が円になっているものを円柱といいます。
円柱を底面に平行に切った場合、どこで切っても切り口は円になり、底面と合同な円になります。
円柱は、電柱やコップ、印鑑などに用いられています。
角錐
「角錐」とは、平面上にある多角形の各点と、その平面上にない1つの点を結んでできる立体のことをいいます。
接していない頂点が1つである面を「底面」、周りの面を「側面」といい、底面と向かい合う頂点との距離が「高さ」です。錐体のうち、対面が多角形になっているものを角錐といいます。底面が三角形であれば三角錐、四角形であれば四角錐です。
角錐には、ティーバッグやテント、ピラミッドなどがあります。
円錐
「円錐」とは、平面上にある円について、“円と同じ平面上にない1つの点を通り、円の円周に交わる線分” が描く曲面と、その円が囲む立体のことです。
円を「底面」、周りの曲面を「側面」といい、1つの頂点と円の距離が「高さ」です。錐体のうち、底面が円になっているものを円錐といいます。
パーティークラッカーや漏斗、盛り塩などが円錐です。
球
「球」とは、1つの点から同じ長さになる点の集まりが、空間上で描く図形のことをいいます。
球はどこを切っても切り口は円になります。球を半分に切ったときの円の中心を「球の中心」、半径を「球の半径」、直径を「球の直径」といいます。
ピンポン玉やビー玉、スーパーボールなどが球です。
体積の求め方
立方体の体積の求め方
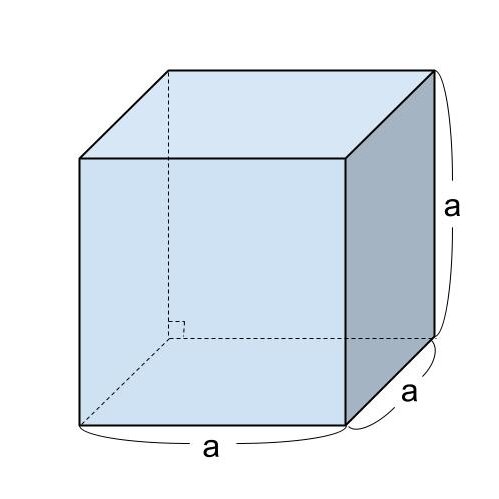
立方体の体積を V 、一辺の長さを a とするとき、立方体の体積は
「V=a×a×a(一辺×一辺×一辺)
=a³」
で求めることができます。
<立方体の体積の公式>
「V=a³」
直方体の体積の求め方
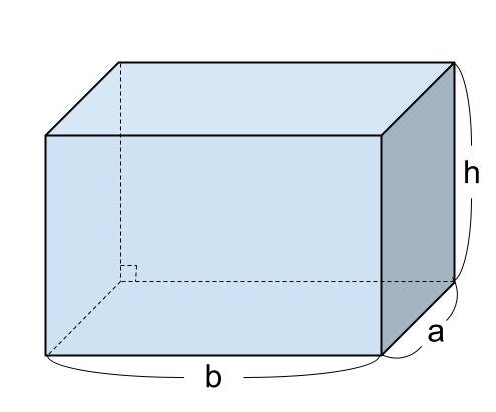
直方体の体積を V 、底面の縦の長さを a 、横の長さを b 、高さを h とするとき、直方体の体積は
「V=a×b×h(縦×横×高さ)
=abh」
で求めることができます。
<直方体の体積の公式>
「V=abh」
角柱の体積の求め方
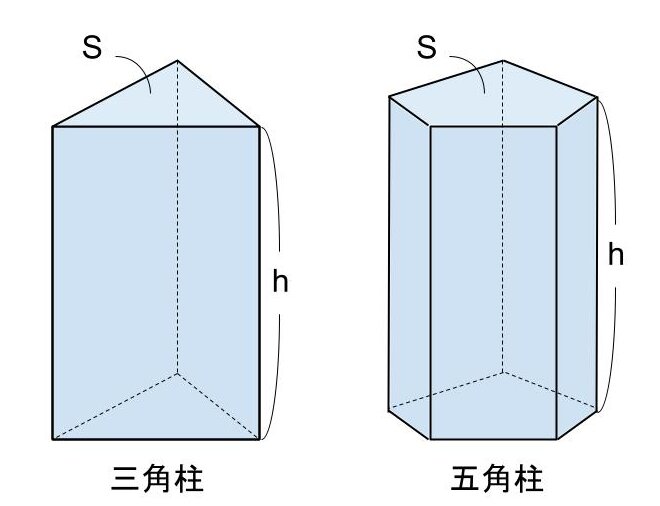
角柱の体積を V 、低面積を S 、高さを h とするとき、角柱の体積は
「V=S×h(低面積×高さ)
=Sh」
で求めることができます。
<角柱の体積の公式>
「V=Sh」
円柱の体積の求め方
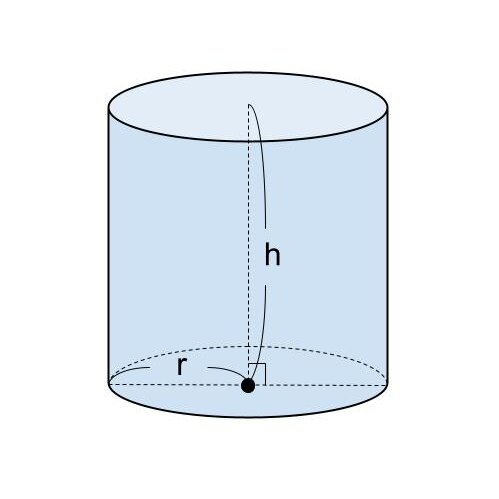
円柱の体積を V 、底面の円の半径を r 、円周率を π 、高さを h とするとき、円柱の体積は
「V=r×r×π×h(半径×半径×円周率×高さ)
=πr²h」
で求めることができます。
<円柱の体積の公式>
「V=πr²h」
角錐の体積の求め方
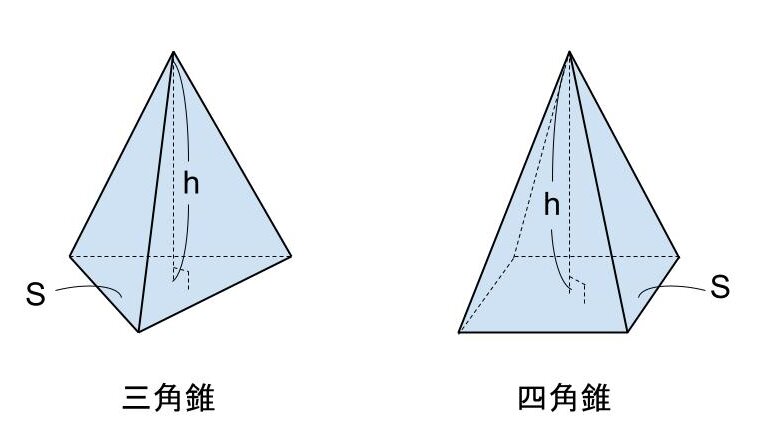
角錐の低面積を S 、高さを h とするとき、角錐の体積は
「V=S×h×1/3(低面積×高さ)
=1/3Sh」
で求めることができます。
<角錐の体積の公式>
「V=1/3Sh」
円錐の体積の求め方
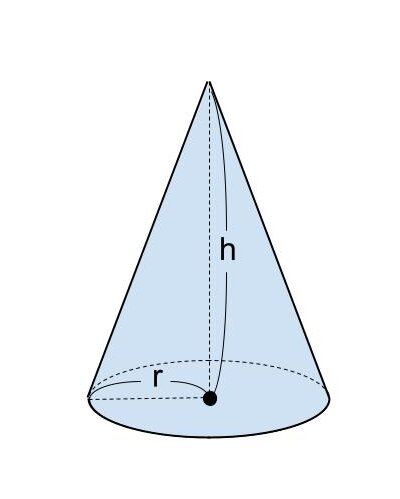
円錐の体積を V 、底面の円の半径を r 、円周率を π 、高さを h とするとき、円錐の体積は
「V=r×r×π×h×1/3
=1/3πr²h」
で求めることができます。
<円錐の体積の公式>
「V=1/3πr²h」
球の体積の求め方
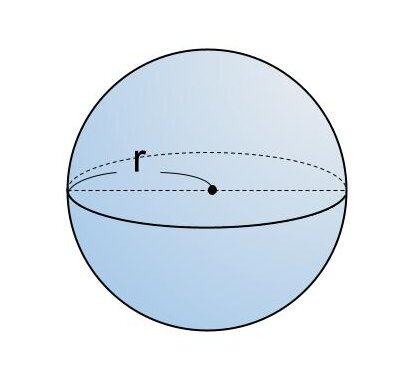
球の体積を V 、半径を r 、円周率を π とするとき、球の体積は
「V=4/3πr³(4/3×円周率×半径の三乗)」
で求めることができます。
<球の体積の公式>
「V=4/3πr³」
体積の問題
立方体の体積の問題
【問題】
一辺が5cmの立方体の体積を求めなさい。
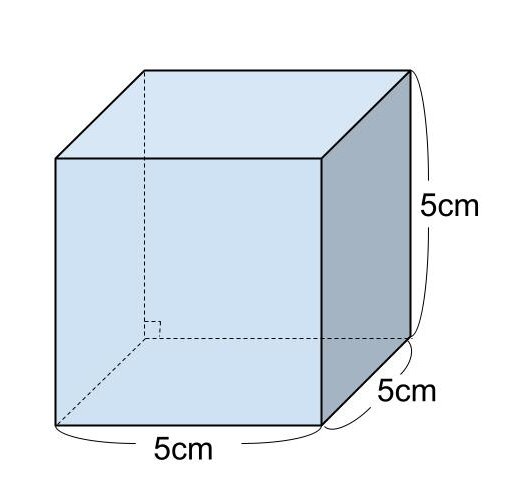
<解答>
立方体の体積を V とする。
V=5³
=125
よって、立方体の体積は125cm³
直方体の体積の問題
【問題】
底面の縦の長さが3cm、横の長さが6cm、高さが4cmの直方体の体積を求めなさい。
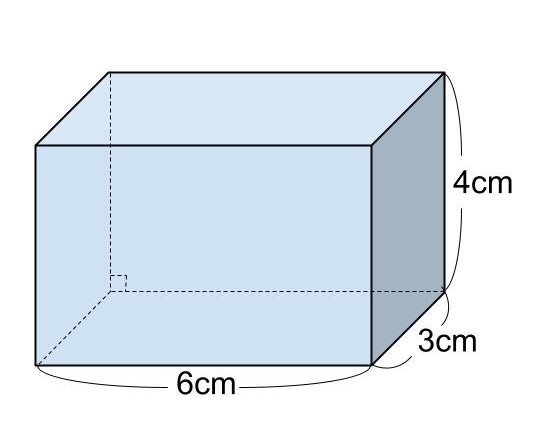
<解答>
直方体の体積を V とする。
V=3×6×4
=72
よって、の体積は72cm³
角柱の体積の問題
【問題】
図のような三角柱と五角柱の体積を求めなさい。
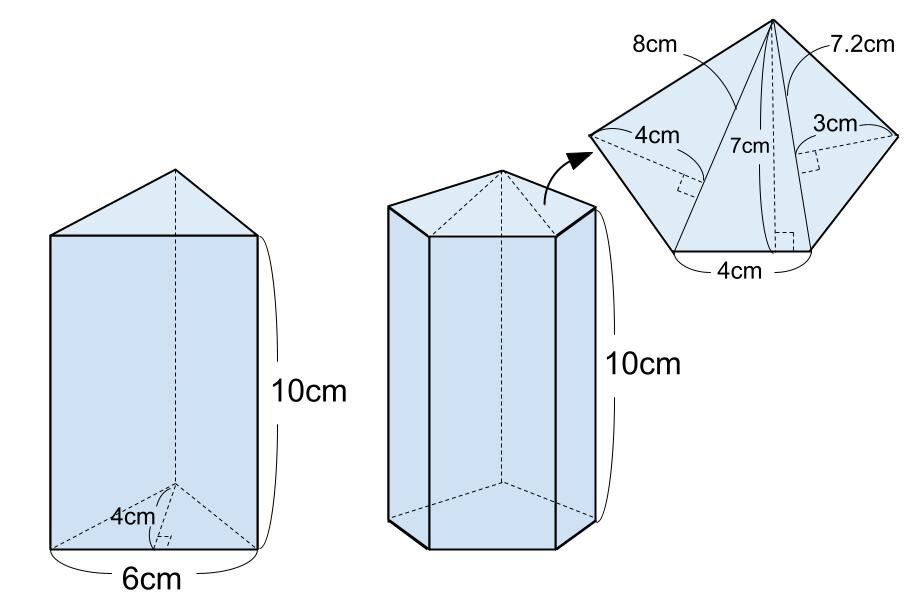
<解答>
三角柱の体積をV₁、五角柱の体積をV₂とする。
V₁=1/2×4×6×10
=120
V₂=(1/2×4×8+1/2×7×4+1/2×3×7.2)×10
=1/2×(32+28+21.6)×10
=5×81.6
=408
よって、三角柱の体積は120cm³、五角柱の体積は408cm³
円柱の体積の問題
【問題】
円周率を π とするとき、半径が3cm、高さ10cmの円柱の体積を求めなさい。
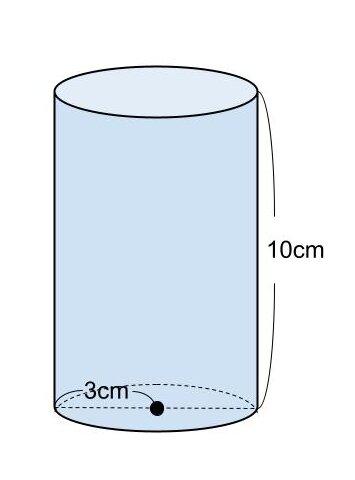
<解答>
円柱の体積を V とする。
V=π×3²×10
=90π
よって、円柱の体積は90πcm³
角錐の体積の問題
【問題】
図のような三角錐と四角錐の体積を求めなさい。
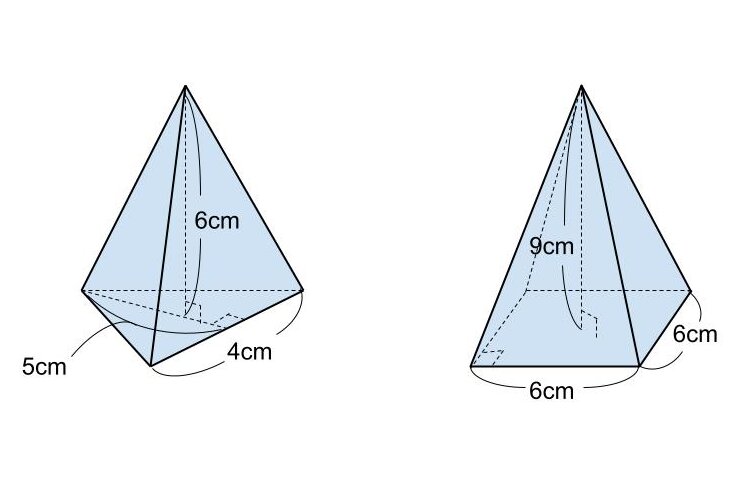
<解答>
三角錐の体積をV₁、四角錐の体積をV₂とする。
V₁=1/3×1/2×4×5×6
=20
V₂=1/3×6×6×9
=108
よって、三角錐の体積は20cm³、四角錐の体積は108cm³
円錐の体積の問題
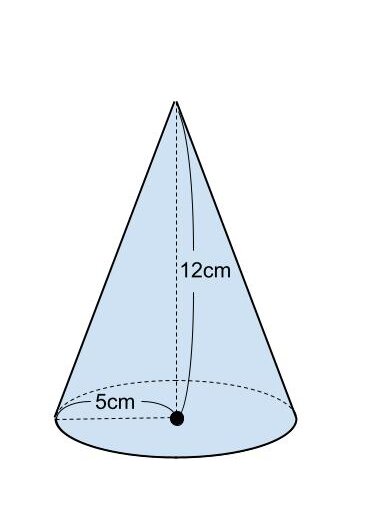
【問題】
円周率を π とするとき、底面の半径が5cm、高さが12cmの円錐の体積を求めなさい。
<解答>
円錐の体積を V とする。
V=1/3π×5²×12
=100π
よって、円錐の体積は100πcm³
球の体積の問題
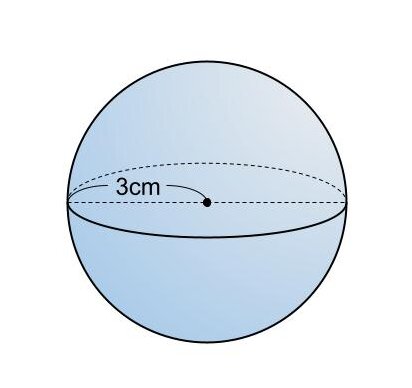
【問題】
円周率を π とするとき、半径が3cmの球の体積を求めなさい。
<解答>
V=4/3π×3³
=4π×9
=36π
よって、球の体積は36πcm³
まとめ
いかがでしたでしょうか。各立体の性質と、その体積の求め方についてご紹介しました。
体積は「低面積×高さ」が基本形ですが、錐体は3で割るという特徴があります。公式を覚えて、立体の体積をマスターしましょう。
さらに体積の求め方を理解するには、個別指導WAMがオススメです。
個別指導WAMは、一人ひとりに合ったカリキュラムや学習アドバイスを通してきめ細かい指導を行っています。
ぜひお気軽にご相談ください。













