こんにちは!個別指導WAMです(^^)/
みなさんは「素数」がどのようなものか理解できていますか?
小学校で初めて習う言葉ですが、中学生になって改めて出てきたときに「なんだっけ?」と思う人もいるのではないでしょうか。
今回の記事ではそんな「素数」についての解説と見分ける方法をご紹介します。
Contents [hide]
素数とは?
素数
「素数」とは〈1より大きい自然数のうち「1」と「その数」でしか割りきれない数〉のことを指します。
英語では「prime number」と呼ばれ、数の中で最も重要視されている数字です。
素数の中で一番小さい数は2です。2は1と2以外では割り切れません。
次の3も3と1以外で割り切れないので素数ですね。
では次の4はどうでしょうか。4は1と2と4で割り切れます。
1と4(その数)以外に2という数字で割り切れるので4は素数ではないと言えます。
4のように素数ではない数のことを「合成数」と言います。
「2」:2÷1=2 2÷2=1 ・・・1と2のみなので素数
「4」:4÷1=4 4÷2=2 4÷4=1・・・1・4以外に2で割り切れるので合成数
素数は何で使うの?
「素数」が〈1より大きい自然数のうち「1」と「その数」でしか割りきれない数〉とわかったところで、「一体どこで使うの?」と思う人もいるのではないでしょうか?
小学生で「素数」というものを習いますが、使うのは中学生になってからです。
では中学内容のどのようなところで使用するのでしょうか。以下で解説します。
●素因数分解
「素数」はまず「素因数分解」に登場します。「素因数分解」とは、「正の整数」を素数の掛け算で表すことです。
例えば〈90〉という数字を素因数分解すると〈2×3×3×5〉となります。
素因数分解なのでこの式以外に解はありません。
〈2×9×5〉でも答えは〈90〉になりますが、これでは不正解です。
何故なら〈9〉という文字は3で割ることができるため、素数ではないからです。
どうでしょうか。
どの数が素数かを理解できていなければ、素因数分解の解にたどりつくことができないことがわかりますね。
●平方根
次に中学3年生で習う「平方根」という単元で使用します。
「平方根」とは「2乗してaとなる数」のことを指します。
例えば〈4〉の平方根は±2となります。
平方根は√(ルート)を用いて表すことができ、〈4〉の場合、√4となります。√4の4を素因数分解すると、√2×2となり、2の二乗となりますね。
この2乗となった数字は√の外に出すことができるので√4=±2となります。
もう一つ〈18〉を例にしてみましょう。
18=√18
√18=√2×3×3(素因数分解)
√2×3×3=√2×3²(数字を整理)
√2×3²=±3√2(2乗となる3を外に出す)
どうでしょうか。平方根の単元の中に素因数分解がでてくることがわかりますね。
素数とはこのような形で使用されます。
素数の見分け方
素数には規則性がなく最大値もわかっていません。
このため、世界中の数学者が素数を解明するために今も研究を続けています。
では、私たちが規則性がない中で素数を見つけるにはどうすればいいのでしょうか。
暗記
実際中学で使用する素数はそこまで大きな数値になることはないため、暗記してしまうというのも一つの手です。100までの素数は以下の通りです。
「2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97」
100までには25個の素数があります。この程度なら頑張れば覚えられそうですね。
割り切れるかどうかで判断する
これも単純な方法です。その数字が1とその数字以外で割り切れるかを考えて判断します。
割り切れなかった場合は素数となります。
確認するときはまずその数値が偶数かどうかを確認しましょう。
偶数であれば2で割り切れるので、素数ではありません。
次に3で割り切れるかどうかをみましょう。
ほとんどはこの2・3で割ることができるので、意外と簡単に素数なのか合成数なのかを見分けることができます。
2・3で割れなかった場合は5、7…と確かめていきます。
その他、〈一の位が5の場合も5で割り切れる〉、〈各桁を足して3の倍数となれば3で割り切ることができる〉といったことは覚えておくと便利かもしれませんね。
エラトステネスのふるい
① 100までの数値を書いた表を用意します。
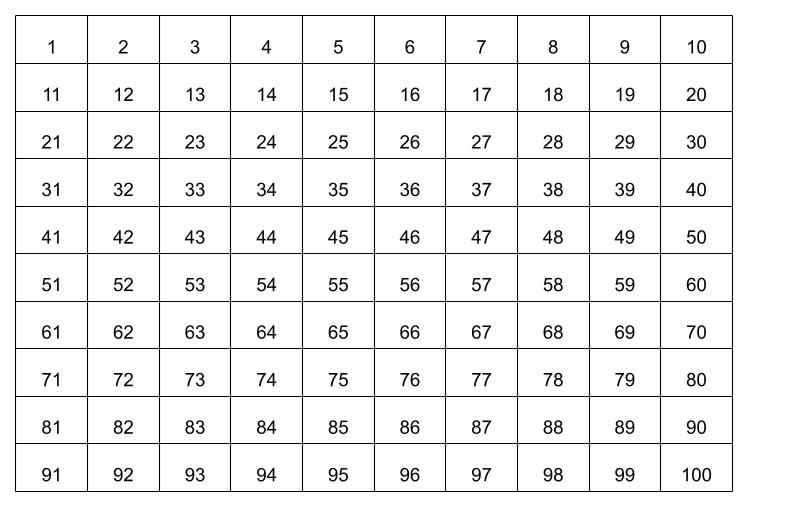
② 1と〈2の倍数〉〈3の倍数〉を削除します。
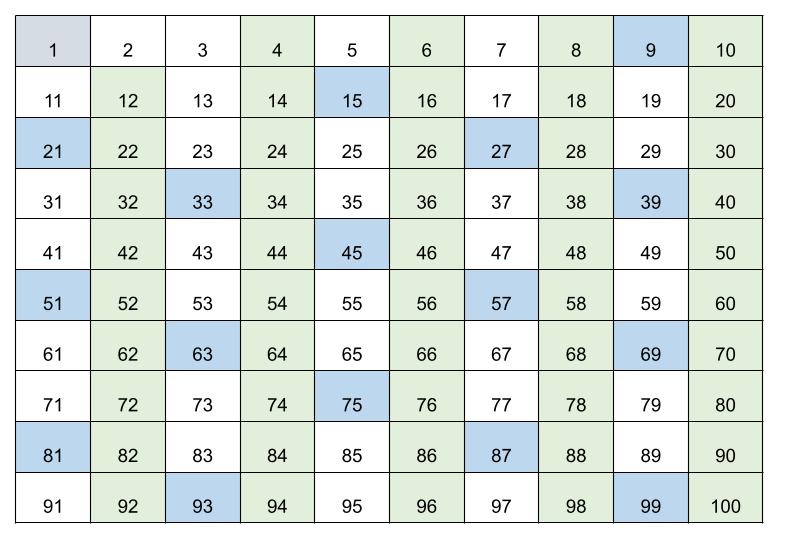
③ 10までの数字の中で残っている5と7の倍数を削除します。
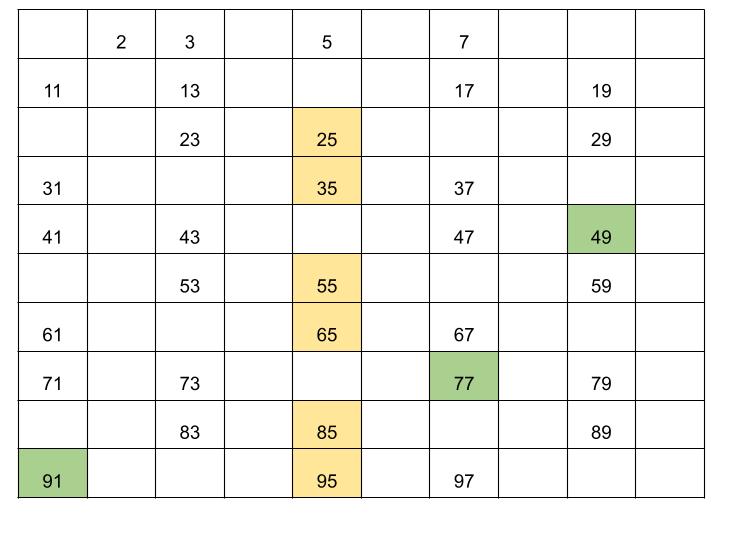
④ 残った数字が素数となります。
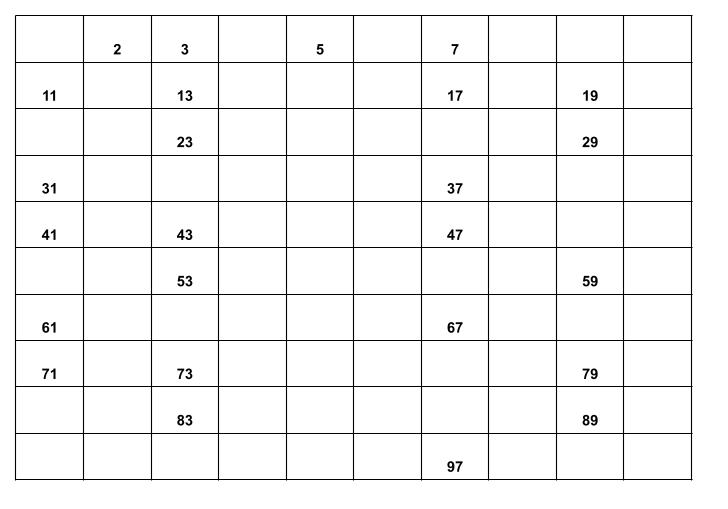
まとめ
いかがでしたか?
「素数」というものは今も研究が続く奥深い数字であることがわかりましたね。
定義をしっかりと理解して、数学の勉強に取り組むようにしましょう。
「もっと素数について知りたい」「素因数分解が理解できない」など素数や数学に関するお悩みをお持ちの方は是非一度個別指導WAMにご相談ください。













