こんにちは!個別指導WAMです(^^)/
本日は【円柱の表面積の求め方は?公式・解くコツ・例題を紹介!】についてお話したいと思います。
この記事を読もうとしている方の中には、「円柱ってどんな図形?」「そもそも表面積って何?」
という方もいらっしゃるのではないでしょうか。
この記事では、それらの疑問にも答えていきます!
最後には問題も用意しています。この機会に円柱の表面積をマスターしましょう!
Contents [hide]
円柱とは
円柱とは
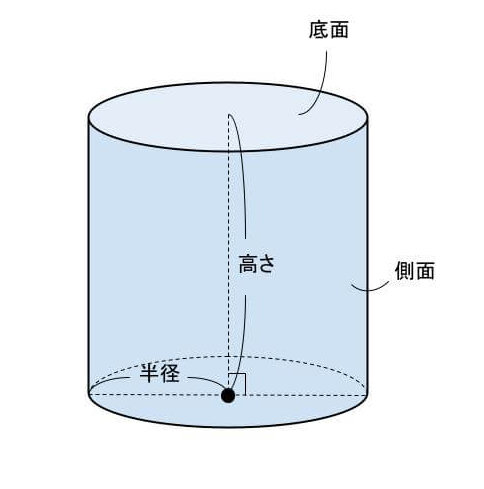
「円柱」とは、2つの平行な平面上にある円について、“2つの円の中心を結ぶ直線に平行で、かつ2つの円の円周に交わる線分” が描く面と、2つの円が囲む立体のことです。 あるいは、長方形の1辺を軸として、その長方形を回転させてできる立体ともいえます。 円柱の向かい合う2つの円を「底面」、周りの曲面を「側面」といい、2つの底面の距離が「高さ」です。底面が円なので、円柱といいます。ほかに、円筒などと呼ばれることもあります。 2つの底面の中心を結ぶ直線が底面に垂直な円柱を「直円柱」、垂直でない円柱を「斜円柱」といいます。一般的に学校で習う円柱は直円柱です。円柱を底面に平行に切るとき、どこを切っても切り口が円になり、底面を含めて合同な円となります。 円柱は、電柱やお菓子のパッケージ、水筒などに用いられています。
表面積とは
表面積とは
「表面積」とは、立体のすべての面の面積を足した値のことをいいます。空気に触れている外側の面の面積の合計、立体を水中に入れたときに濡れる部分の面積の総和、という言い方もできます。表面積は、底面の面積と側面の面積を足したものであることが多くなっていますが、その立体によって求め方が変わってくることが特徴です。
円柱の表面積の公式
円柱の表面積の公式
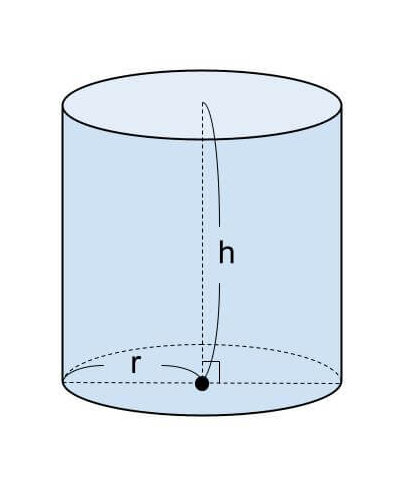
円柱の表面積を S 、底面の円の半径を r 、円周率を π 、高さを h としたとき、円柱の表面積は 「S=2πr²+2πrh<2×円周率×半径×半径+2×円周率×半径×高さ> =2πr(r+h)<2×円周率×半径×(高さ+半径)>」 で求めることができます。
S は “surface area(表面積)” 、r は “radius(半径)” 、h は “height(高さ)” の頭文字です。
<円柱の表面積の公式> S=2πr(r+h)
円柱を展開して求める
表面積は平面に関することなので、立体である円柱を平面にするとわかりやすくなります。
そこで、展開図を描いてみましょう。円柱を展開すると、2つの合同な円(2つの底面)と、長方形(側面)に分かれます。
つまり、円柱の表面積を求めるには、2つの合同な円(2つの底面)と、長方形(側面)の面積を足せばよいのです。

円柱の表面積をS₁、底面の面積をS₂、側面の面積をS₃、半径を r 、円周率を π 、高さを h としたとき、S₂=r×r×π =πr²
長方形(側面)の縦の長さは円柱の高さ、横の長さは底面の円周の長さになります。
円周の長さは、直径×円周率で求めることができます。
S₃=h×(r×2×π)
=2πrh
円柱の表面積は、2つの合同な円(2つの底面)と、長方形(側面)の面積の和なので、
S₁=S₂×2+S₃
=πr²×2+2πrh
=2πr²+2πrh
=2πr(r+h)
となり、円柱の展開図から円柱の表面積の公式を導くことができました。
円柱の表面積の問題
問題①
【問題①】
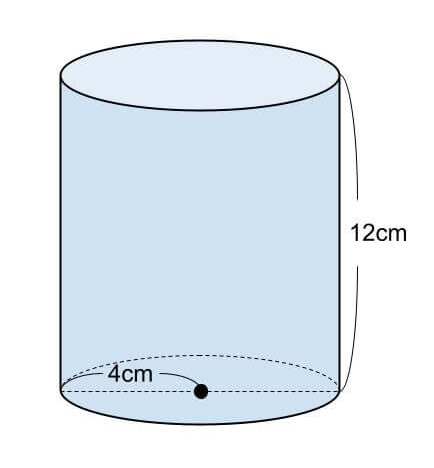
半径が4cm、高さ12cmの円柱の表面積を求めなさい。
<解答>
円柱の展開図は下図のようになる。
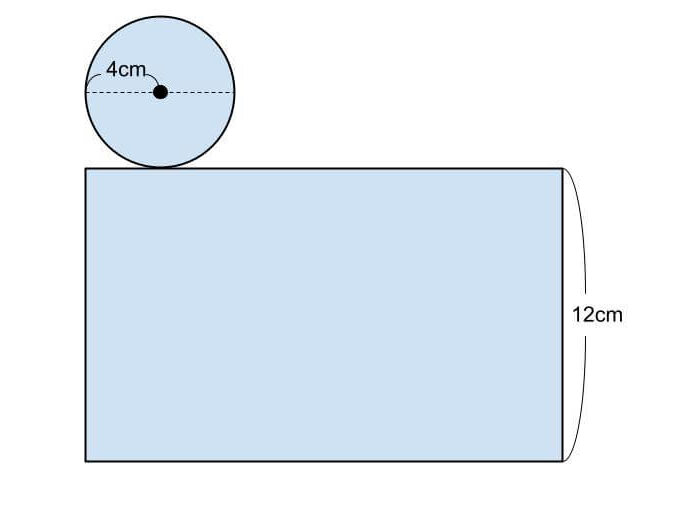
柱の表面積をS₁、底面積をS₂、側面積をS₃、とする。円柱の表面積は2つの低面積と側面積の和なので、
S₁=2S₂+S₃ …①
S₂=4×4×π
=16π …②
展開図において長方形の横の長さをℓとすると、
ℓ=4×2×π
=8π
S₃=12×8π
=96π …③
②、③を①に代入して、
S₁=2S₂+S₃
=16π×2+96π
=32π+96π
=128πよって、円柱の表面積は128πcm²
問題②
【問題②】
左図のような長方形ABCDがある。長方形ABCDを、直線ABを軸に1回転させてできる立体の表面積を求めなさい。
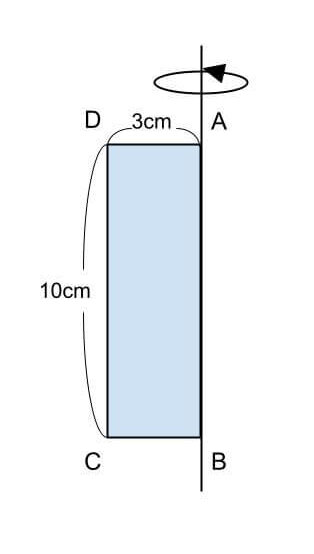
<解答>
長方形ABCDを直線ABを軸に1回転させてできる立体と、その展開図は下図のようになる。
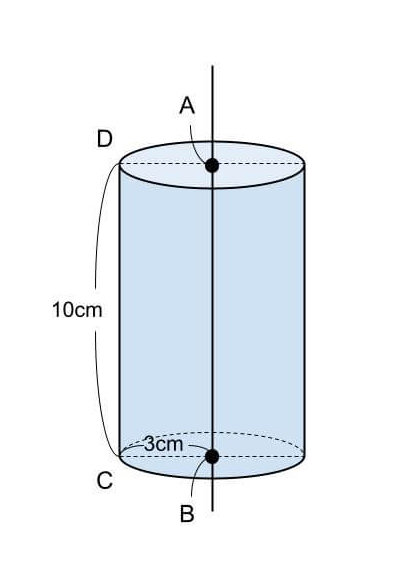
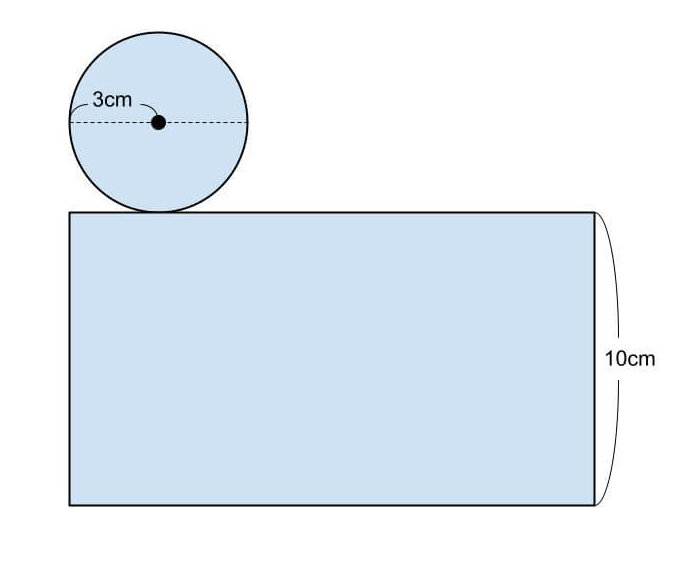
円柱の表面積をS₁、底面積をS₂、側面積をS₃、とする。
円柱の表面積は2つの低面積と側面積の和なので、
S₁=2S₂+S₃ …①
S₂=3×3×π
=9π …②
展開図において長方形の横の長さをℓとすると、
ℓ=3×2×π
=6π
S₃=10×6π
=60π …③
②、③を①に代入して、
S₁=2S₂+S₃
=2×9π+60π
=18π+60π
=78π
よって、円柱の表面積は78πcm²
まとめ
いかがでしたか?
円柱の表面積は展開図を描いて考えるとわかりやすくなります。
公式も、この考え方を知っていると簡単に覚えることができるでしょう。
繰り返し問題を解いて、円柱の表面積をマスターしましょう!(^^)
さらに円柱の表面積を理解するには、個別指導WAMがオススメです。
個別指導WAMは、一人ひとりに合ったカリキュラムや学習アドバイスを通してきめ細かい指導を行っています。ぜひお気軽にご相談ください。













