こんにちは!個別指導WAMです(^^)/
今回は「球の体積」についてお話します。
みなさんは球の体積の求め方を知っていますか?
この記事を読もうとしている方の中には、
「球の体積の公式は?」「円とは違うの?」「そもそも体積って何?」
という方もいらっしゃるのではないでしょうか。
この記事では、それらの疑問に答えていきます。
最後には問題も用意しています。
この機会に球の体積をマスターしましょう!
Contents [hide]
円と球の違い
円とは
「円」とは、平面上で、1つの点から同じ長さになるように描いた丸い形のことです。
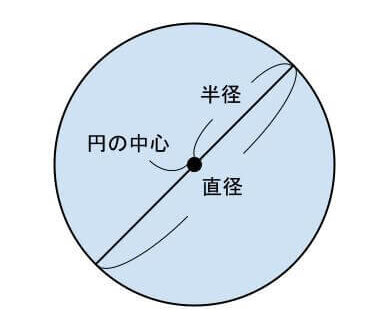
コンパスで描いたような丸い形で、円の真ん中の点(コンパスの針を刺した部分)を「円の中心」、中心と円の周り(円周)を結ぶ直線を「半径」といいます。
円周から円周まで引いた直線のうち、中心を通るものを「直径」といい、これが円の内部にある直線の中で最も長くなります。
中心から同じ距離にある点の集まりが円であるため、同じ円の半径・直径の長さは常に同じです。
円は時計やCD・DVD、道路の標識などに用いられています。
球とは
「球」とは、空間において、1つの点から同じ長さになる点の集まりをいいます。
円は平面図形ですが、球は立体図形です。
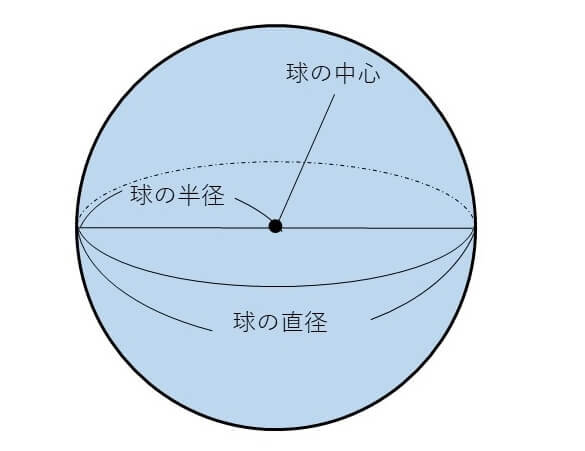
球は、どこで切っても切り口が円になります。球を半分に切ったときの切り口が一番大きな切り口です。
円と区別するため、球を半分に切ったときの円の中心を「球の中心」、半径を「球の半径」、直径を「球の直径」といいます。
テニスボールやビー玉、シャボン玉などが球となっています。
体積とは
体積とは
「体積」とは、立体の嵩(かさ)のことをいいます。
空間においてその物体が占めている場所の大きさのことで、中身が詰まっているものの大きさ、ともいえます。
単位は、「cm³(立方センチメートル)」「m³(立方メートル)」「l(リットル)」などになります。
体積は、容器の容量を表す「容積」とは異なります。
容積は、その物体にどのくらい入るかという量のことで、単位は「cc(シーシー)」「ml(ミリリットル)」「l(リットル)」などになります。
球の体積の公式
球の体積の公式
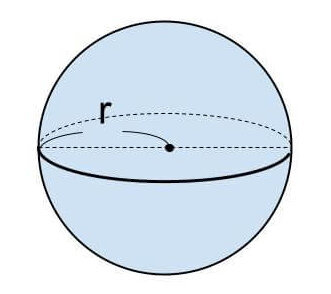
球の体積を V 、半径を r 、円周率を π としたとき、球の体積は
「V=4/3πr³(4/3×円周率×半径の三乗)」
で求めることができます。
V は “volume(体積)” 、r は “radius(半径)” の頭文字です。
<球の体積の公式>
「V=4/3πr³」
分数や累乗があり、少しややこしいですね。
そこで、「身の上に心配アール三乗」という語呂合わせがあります。
“ 身(3) ” の上に “ 心配アール三乗(4πr³) ” です。
公式が覚えられない方は語呂合わせで覚えましょう。
円錐・円柱との関係から求める
球の体積は、円柱・円錐の体積との間に独特な関係性があります。
これを覚えておくと、公式を忘れても体積を導き出すことができます。
それではまず、その球がぴったり収まる円柱、つまり「球の直径」の長さを「底面の直径」「高さ」とする円柱の体積は、その球の体積の3/2になるということです。
逆にいえば、同条件において、球の体積は円柱の体積の2/3ということになります。
同様に、「球の直径」の長さを「底面の直径」「高さ」とする円錐の体積は、球の体積の半分となり、円柱の体積の1/3となります。
つまり、下の図のような円錐・球・円柱には、 「円錐の体積 : 球の体積 : 円柱の体積=1 : 2 : 3」 という特徴があります。
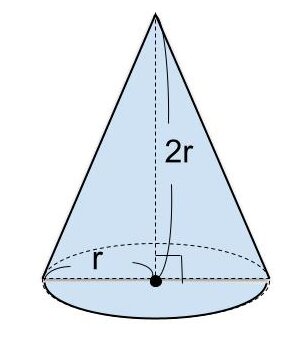
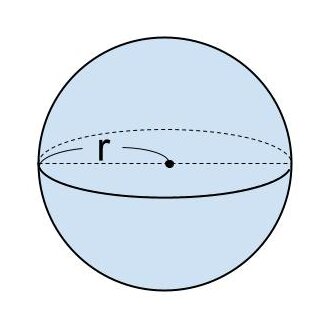
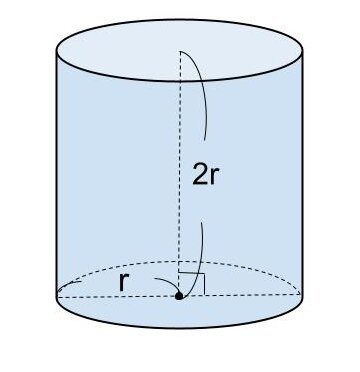
ここで、球の体積をV₁、円柱の体積をV₂、球の半径を r 、円周率を π としたとき、
この場合の円柱の体積(V₂)は、
V₂=r×r×π×2r(半径×半径×円周率×高さ)
=2πr³
先ほどの特徴を活用すると、球の体積(V₁)は
V₁=V₂×2/3
=2πr³×2/3
=4/3πr³
となり、円柱の体積から球の体積の公式を導くことができました。
球の体積の問題
問題①
<解答>
半径 r の球の体積 V は
V=4/3πr³
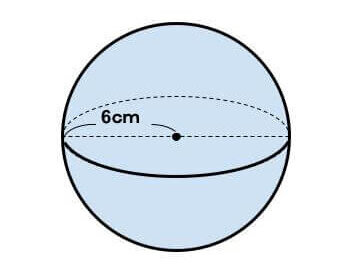
r=6(cm)より、
V=4/3π×6×6×6
=288π(cm³)
よって、体積は288πcm³
問題②
底面の半径が6cm、高さが10cmの円柱状の水槽に、高さ7cmまで水が入っている。
この水槽に半径が9/2cmの鉄球を入れたとき、水槽からあふれる水の量を求めなさい。
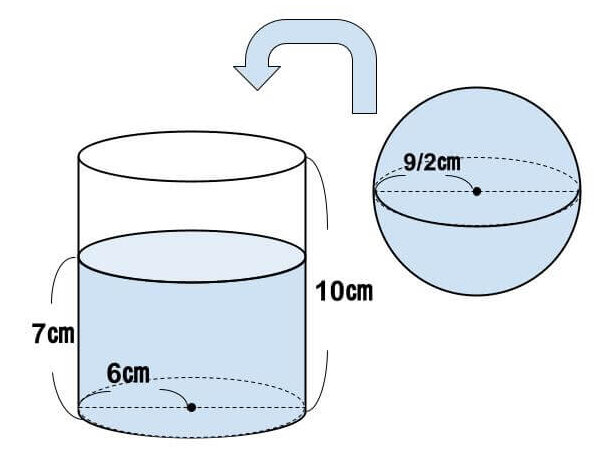
<解答>
鉄球の体積をV₁、水槽の水が入っていない部分の体積をV₂とする。
V₁=4/3π×(9/2)³
=π×3×9×9/2
=243/2π(cm³)
V₂=6×6×π×(10-7)
=108π(cm³)
鉄球の体積から、水槽の水が入っていない部分の体積を引いて
V₁-V₂=243/2π-108π
=27/2π(cm³)
よって、水槽からあふれる水の量は27/2πcm³
まとめ
いかがでしたでしょうか。
円と球の違い、球の体積についてご紹介しました。
球の体積には、球がちょうどぴったり入る大きさの円柱の体積の2/3になるという性質もあり、覚えておくと便利です。
公式を覚えて、球の体積をマスターしましょう。
さらに球の体積の公式を使いこなすには、個別指導WAMがオススメです。
個別指導WAMは、一人ひとりに合ったカリキュラムや学習アドバイスを通してきめ細かい指導を行っています。
ぜひお気軽にご相談ください。