こんにちは!個別指導WAMです(^^)
今回は、『中点連結定理とは?三角形・台形・四角形の証明をわかりやすく解説』についてご紹介します。
皆さんは「中点連結定理」を覚えていますか?
あるいは、これから学校で習うという人もいるかもしれません。
中点連結定理は、図形問題で役に立つことが多い数学の定理です。
難しいものではないので、この記事を通して中点連結定理の使い方や証明の仕方を理解していきましょう。
Contents [hide]
中点連結定理とは
中点連結定理とは、中学3年生の範囲で習う平面幾何の定理の一つです。
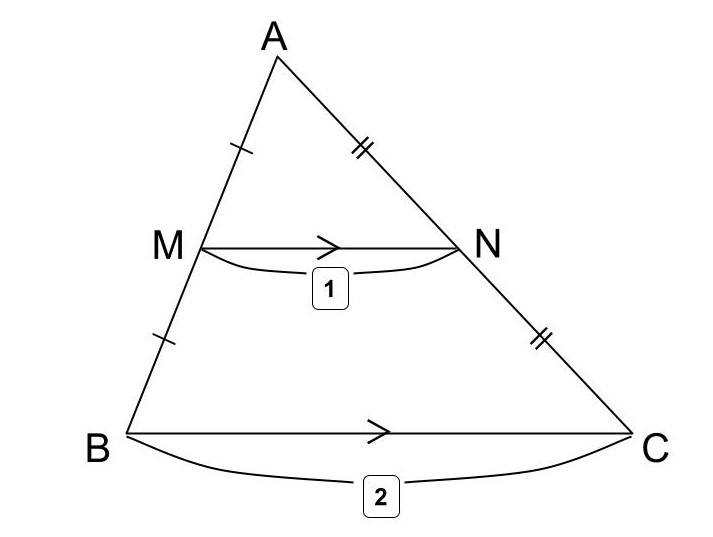
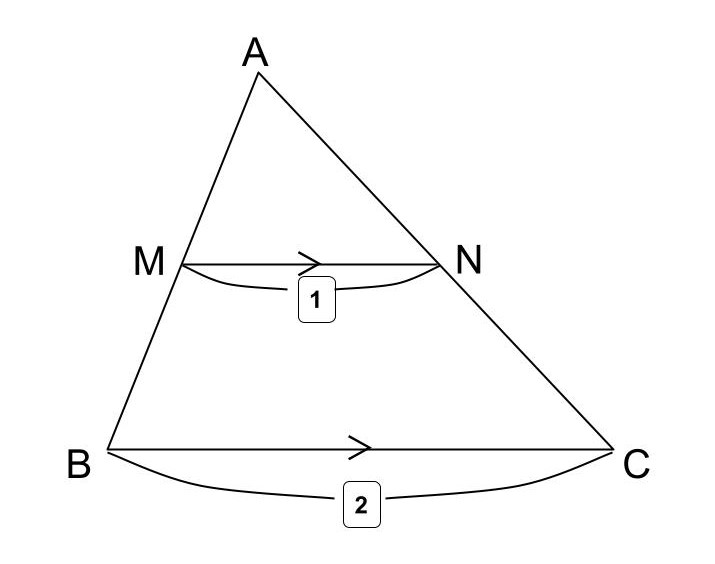
上の△ABCの2辺AB、ACの中点M、Nを連結した線分MNについて、次のような定理が成り立ちます。
中点連結定理:
「△ABCの2辺AB、ACの中点をそれぞれM、Nとすると、MN//BC、MN=1/2BC」
また、△ABCの2辺AB、ACの中点M、Nを結んでできる△AMNについて、次のようなことが言えます。
「△AMN∽△ABC、△AMN:△ABC=1:2」
三角形の底辺を除く2辺の中点を結んだ線分、つまり中点連結は、底辺と平行かつ底辺の半分の長さとなります。
また、相似比が1:2の相似な三角形ができます。
中点連結定理の証明(三角形)
それでは、
中点連結定理:
「△ABCの2辺AB、ACの中点をそれぞれM、Nとすると、 MN//BC、MN=1/2BC」
が成り立つことを証明してみます。
この証明方法には、
・三角形の相似を利用した方法
・平行四辺形の性質を利用した方法
の2種類があります。以下に各方法による証明の仕方をご説明します。
相似を利用した中点連結定理の証明
【証明① 三角形の相似を利用】
手順:
[1] △ABCと△AMNが相似の関係にあることを説明する。
[2] 辺MN、BCの関係を説明する。
<証明>
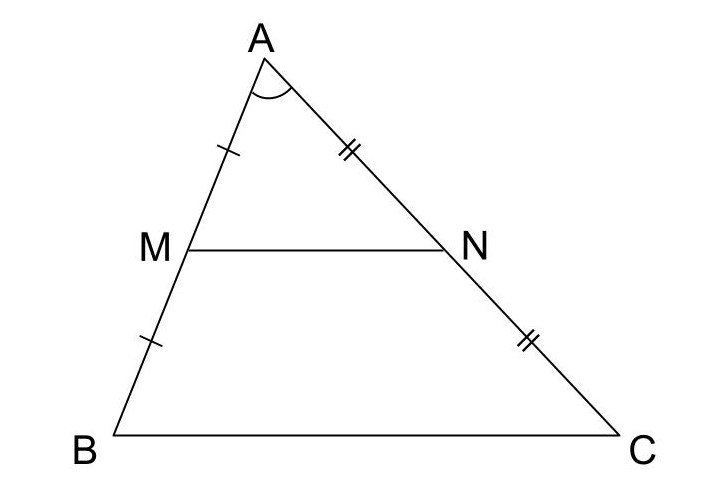
△ABCと△AMNにおいて、
点M、Nはそれぞれ辺AB、ACの中点なので、
AB:AM=2:1 …①
AC:AN=2:1 …②
∠Aは共通なので、
∠BAC=∠MAN …③
①、②、③より、 2組の辺の比とその間の角が等しいので、
△ABC∽△AMN
相似な図形の対応する角は等しいので、
∠ABC=∠AMN
同位角が等しいので
MN//BC …④
また、①より、
△ABC:△AMN=2:1なので、
MN=1/2BC …⑤
よって、
④、⑤より、中点連結定理が成り立つ。
平行四辺形を利用した中点連結定理の証明
【証明② 平行四辺形の性質を利用】
手順:
[1] 平行四辺形の性質である「対角線がそれぞれの中点で交わる」を利用して、△ABCの辺CAを対角線にもつ四角形AMCDが平行四辺形であることを説明する。
[2] [1]を利用して、四角形MBCDが平行四辺形であることを説明する。
<証明>
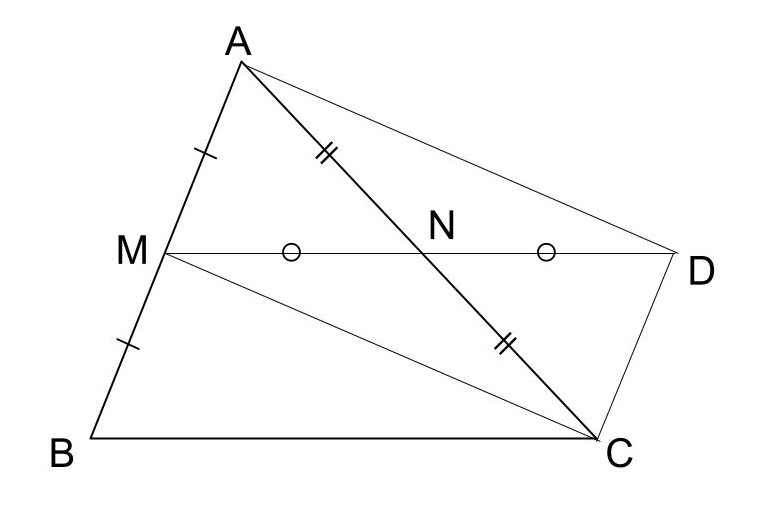
△ABCにおいて、MNの延長線上にMN=NDとなる点Dをとる。
四角形AMCDにおいて、
MN=ND、AN=NCより、
対角線がそれぞれの中点で交わるので、四角形AMCDは平行四辺形である。
よって、
AM=CD
AM//CD …①
また、四角形MBCDにおいて、
①より、MB//CD …②
AM=MBよりMB=CD …③
①、②より、
1組の対辺が平行かつ長さが等しいので、四角形MBCDは平行四辺形である。
よって、
MN//BC …④
MN=1/2BC …⑤
④、⑤より、中線連結定理が成り立つ。
中点連結定理の逆の証明
中点連結定理は、その仮定と結論を入れ替えた場合も成立します。
これを「中点連結定理の逆」と言います。
中点連結定理の逆:
「△ABCの辺AB上の点Mと、辺AC上の点Nについて、
MN//BC、MN=1/2BCであれば、点M、Nはそれぞれ辺AB、ACの中点となる。」
中点連結定理の逆も、中点連結定理と同様に、三角形の相似を利用して証明することができます。
以下に証明の仕方をご説明します。
中点連結定理の逆の証明
手順:
[1] MN//BCをもとに三角形の相似条件である「2つの角がそれぞれ等しい」を利用し、△AMNと△ABCが相似であることを説明する。
[2] MN=1/2BCをもとに相似比を利用し、点M、NがそれぞれAB、ACの中点であることを説明する。
<証明>
△AMNと△ABCにおいて、
MN//BC …①
MN=1/2BC …②
と仮定する。
①より、平行線の同位角は等しいので、
∠AMN=∠ABC …③
∠ANM=∠ACB …④
③、④より、2つの角がそれぞれ等しいので、
△AMN∽△ABC
また、②より、
MN:BC=1:2なので、
△AMN:△ABC=1:2
よって、
AM:AB=1:2
AM=MBなので、点MはABの中点となる。 …⑤
同様に、AN:AC=1:2
AN=NCなので、点NはACの中点となる。 …⑥
⑤、⑥より、中点連結定理の逆が成り立つ。
中点連結定理の証明(台形)
中点連結定理の問題は、一般的に三角形を用いたものがほとんどですが、台形の中点連結定理も三角形と同様に成り立ちます。
台形の中点連結定理:
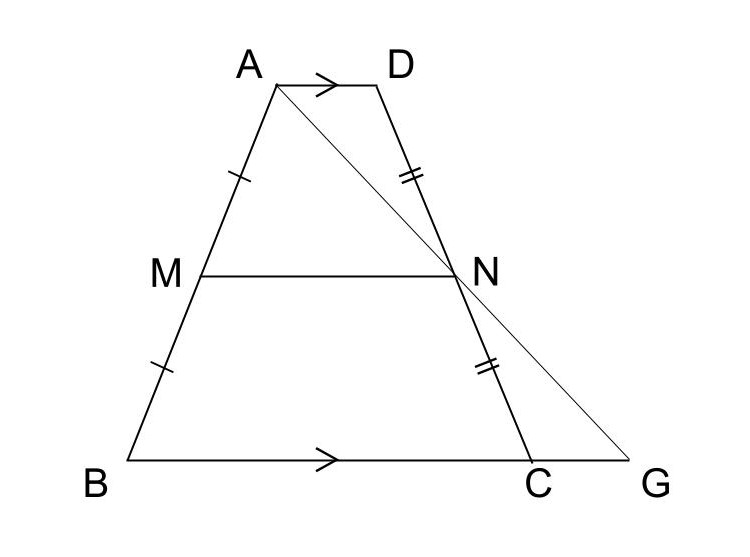
「台形ABCDにおいて、辺AB、DCの中点をそれぞれ点M、Nとすると、
AD//BCであれば、MN//BC、MN=(AD+BC)/2」
以下に証明の仕方をご説明します。
台形の中点連結定理の証明
手順:
[1] 台形ABCDのBCの延長線上点Gをおき、△NDAと△NCGが合同であることを説明する。
[2] 三角形の合同条件である「合同な図形の対応する辺の長さは等しい」と、△ABGにおける中点連結定理を利用し、MNがADとBCの和の半分であることを説明する。
<証明>
台形ABCDにおいて、BCの延長線上とAMの交点を点Gとする。
△NDAと△NCGにおいて、
対頂角が等しいので、
∠AND=∠GNC …①
点NはDCの中点なので、
DN=CN …②
AD//BCかつ点GはBCの延長線上にあるので、
AD//CG
平行線の錯角が等しいので、
∠NDA=∠NCG …③
①、②、③より、
1辺とその両端の角がそれぞれ等しいので、
△NDA≡△NCG
よって、合同な図形の対応する辺の長さは等しいので、
AN=GN …④
AD=GC …⑤
△ABGにおいて、
④より、点Nは辺AGの中点である。
BG=BC+CGなので、⑤より、
BG=AD+BC …⑥
点M、Nはそれぞれの辺AB、GAの中点なので、中点連結定理より、
MN=1/2BG …⑦
⑥を⑦に代入して、
MN=1/2(AD+BC)
よって、台形の平行でない対辺の中点を結んだ線分は、上底と下底を合わせた長さの半分となり、
台形の中点連結定理として
MN=1/2(AD+BC)
が成り立つ。
中点連結定理の証明(四角形)
中点連結定理を利用すると、四角形の中点を結ぶと平行四辺形になるということを証明することもできます。
四角形の中点連結定理:
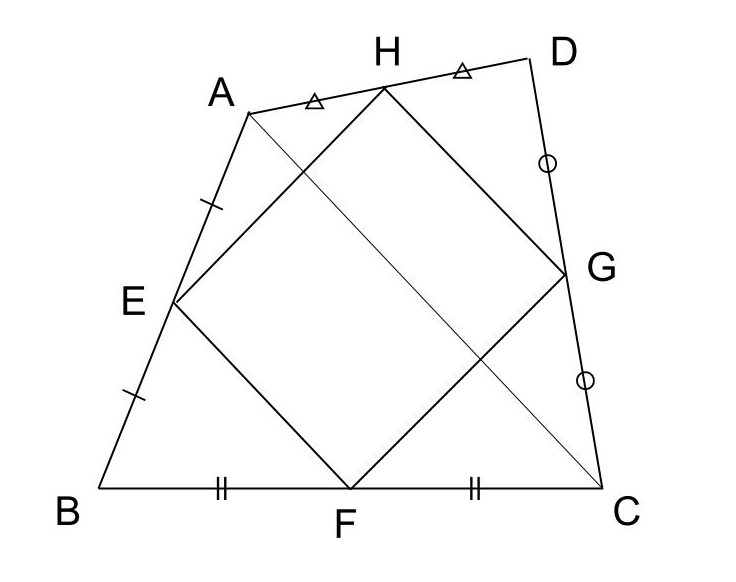
「四角形ABCDの4辺AB、BC、CD、DAの中点をそれぞれ点E、F、G、Hとしたとき、
四角形EFGHは平行四辺形となる。」
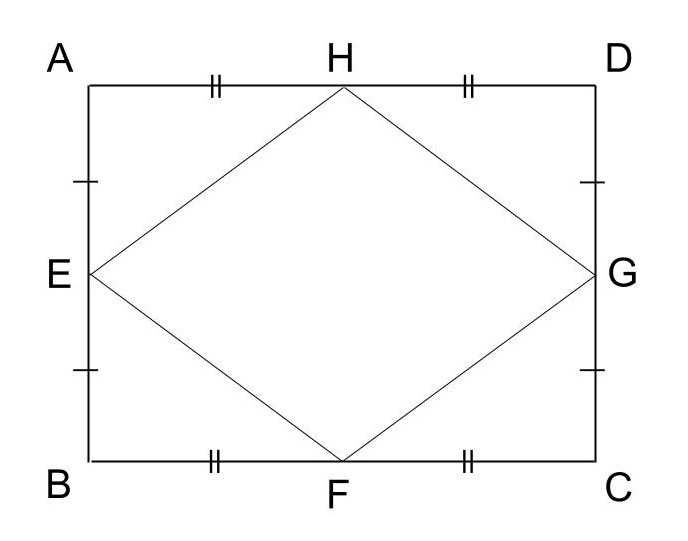
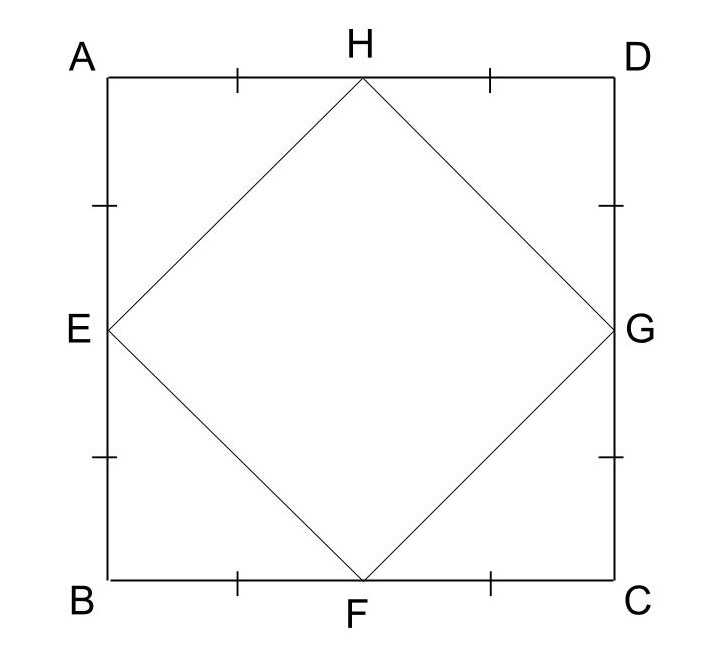
四角形ABCDが長方形の場合はひし形、正方形の場合は正方形となります。
四角形の中点連結定理の証明では、三角形を利用します。以下に証明の仕方をご説明します。
手順:
[1] 対角線を1本引き、2つの三角形において中点連結定理を利用して、四角形EFGHの対辺の関係を説明する。
[2] 平行四辺形になるための条件である「1組の対辺が平行かつ長さが等しい」を利用して、四角形EFGHが平行四辺形であることを説明する。
<証明>
対角線ACを引く。
△ABCにおいて、点E、FはそれぞれAB、BCの中点なので、中点連結定理より、
EF//AC …①
EF=1/2AC …②
△ACDにおいて、点G、HはそれぞれCD、DAの中点なので、中点連結定理より、
HG//AC …③
HG=1/2AC …④
①、③より、
EF//HG …⑤
②、④より、
EF=HG …⑥
⑤、⑥より、1組の対辺が平行かつ長さが等しいので、四角形EFGHは平行四辺形である。
まとめ
いかがでしたか。
中点連結定理について、三角形・台形・四角形の証明を解説しました。
最後におさらいしてみましょう。
中点連結定理:
「△ABCの2辺AB、ACの中点をそれぞれM、Nとすると、MN//BC、MN=1/2BC」
台形や他の四角形についても、この基本を利用することで証明することができます。
問題演習を繰り返して、しっかりと身に付けておきましょう。
中点連結定理の理解をさらに深めるには、個別指導塾がオススメです。
個別指導WAMでは、一人ひとりに合わせた指導を行っているため、丁寧に学習を進めることができます。
ぜひ個別指導WAMにご相談ください。