こんにちは!個別指導WAMです(^^)/
今回は【球(円)の表面積の求め方!公式を簡単に覚えるコツと考え方】についてお話したいと思います。
数学で外せないのが、図形問題です。しかし、図形問題が苦手、好きではない、理解できない、という学生も多いのではないでしょうか。立体図形の表面積は、中学生で習う単元です!今回は立体図形の中でも、球(円)の表面積について解説していきます。
学校で習ったけどよく分からない、という人はぜひ一度この記事を読んで、学習の参考にしてみてください!
表面積の基礎知識
そもそも表面積の意味を知っていますか?
表面積とは、立体を形成する全ての表面の面積を合計した面積のことです。
「底面と側面を足した面積」、「立体を平面上に広げてできる展開図の面積」とも言われています。表面積の計算は立体の種類に合わせて計算方法を変える必要があります!
表面積の計算は通常、立体の底面の面積「底面積」と立体の側面の面積「側面積」を足すことで求めることができます。しかし、立体の形が錐体なのか柱体なのかによって底面積が1つの場合と、2つの場合が存在しており、計算方法が異なるということは分かりますよね?
ここまで表面積の求め方を「底面積」+「側面積」が通常と説明してきましたが、球などの形状が特殊な立体の場合ではどうなのでしょうか?その場合は、通常の「底面積」+「側面積」という方法では求めることができません。そのため、解き方には注意が必要となるのです!
球でイメージしやすいのはボールですが、ボールには角や辺がなく、まるい形をしています。そのため、球の表面積の求め方が「底面積」+「側面積」に当てはまらない、ということが分かりますね?
球の表面積の公式は?
球の表面積の公式
球の表面積を求めるための公式があります。
球の表面積=半径×半径×π(円周率)×4=4πr² となります。
公式を覚えておくことで、簡単に球の表面積を求めることができます!しかし、この公式を証明するのは非常に難しく、高校生でも難しいと言われています。そのため、公式は正確に覚えておくことが大切です!
ここで円柱の側面積の計算方法を思い出してみてください。
円柱の底面の円の半径がr、高さをhとします。円柱の側面積は、底面の円周×高さで求めることができますよね?
底面の円周=直径(2r)×円周率(π)なので2πrとなり、側面積は、2πr(底面の円周)×h(高さ)=2πrhとなります。
その円柱の中に、半径rの球がピッタリ収まっているとします。
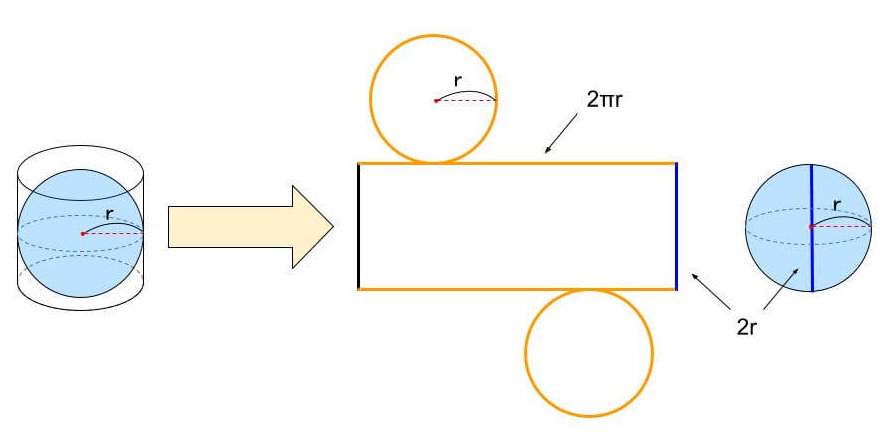
そうすると、先程の円柱の高さが球の直径になることが分かりますよね?
球の直径は2rとなり、上で求めた円柱の側面積「2πrh」のh(高さ)を2r(球の直径)に置き換えると2πr×2r=4πr²となり、球の表面積の公式と同じになります!
つまり、球の表面積とその球がピッタリ収まる円柱の側面積が同じになるということが分かります。
【例題】球の表面積の求め方
それでは例題を2問挙げてみます!難しい問題ではないので、公式を使って一緒に解いてみましょう。
【例題1】 半径5㎝の球の表面積を求める。
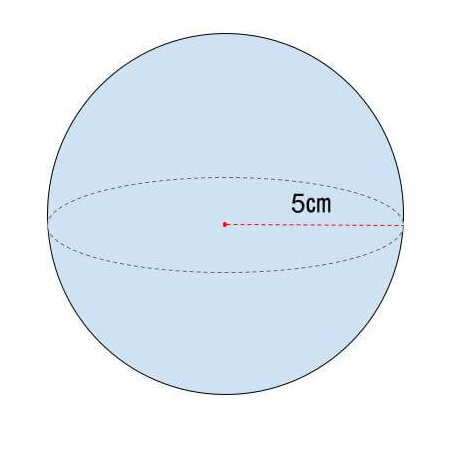
公式は、半径×半径×円周率×4=4πr² なので
5×5×π×4=100π
答えは100π㎠ となります。
とっても簡単ですね!
【例題2】 半径6㎝の半球の表面積を求める。
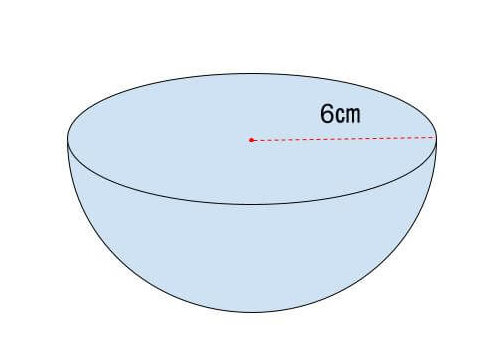
次は半球の表面積を求める問題です。
使う公式は同じなので、半径×半径×円周率×4=4πr² となり
6×6×π×4=144π ですが、球の半分なので1/2にする必要があります。
144π×1/2=72π となりますね!
ここで見落としてはいけないのが、半径6㎝の円の面積が必要であるということです!
円の面積の求め方は、半径×半径×πなので 6×6×π=36π となります。
合計は72π+36π=108π
答えは108π㎠ となります。
公式を知っておくだけで、簡単に球の表面積の計算ができますね!
まとめ
ここまで球の表面積について解説してきましたが、いかがでしたか?
公式を覚えることで簡単に表面積を求めることができるため、必ず覚えるようにしましょう。
図形問題についてもっと詳しく勉強したいという方、勉強に対して不安を感じている方は、ぜひ個別指導WAMに気軽にご相談ください。学習支援全般のお手伝いをさせていただきます!













