皆さん、こんにちは!個別指導塾WAMです(^^)/
本日は【図形の三角形】についてお伝えします!
図形問題でも頻繁に出題される三角形ですが、様々な種類や定理があるため、実は複雑なんです…!
この記事では三角形とは『どんな図形、辺の長さ、角度の定理、種類』などをご紹介します。
ぜひ参考にしてください!
Contents [hide]
【三角形の定義】
三角形とは3つの線からなる図形です。
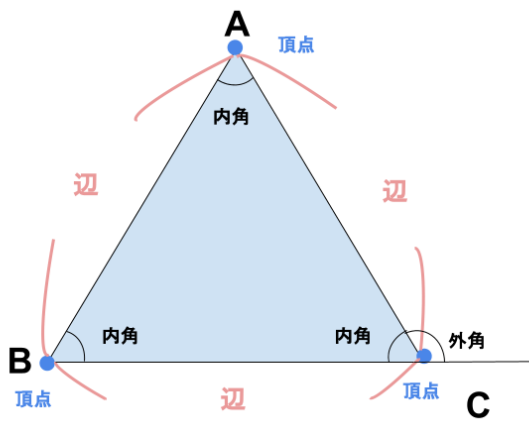
3つの点を頂点、3つの線分を辺といいます。
2つの辺がなす角を内角、外側にできる角を外角といいます。
三角形には以下の特徴があります。
・すべての三角形の内角の和は必ず 180°
・2つの辺の長さの和は残りの1つの辺の長さより大きく、2つの辺の長さの差は残りの1つの辺の長さより短い
・三角形の辺の大小関係は、その向かい合う角の大小関係と一致
・外角は、それととなり合わない2つの内角の和と等しい
上記の図形を例に、点A、点B、点Cを結んだ三角形は△ABC、角度は∠Aと表記します。
また、∠Aは2つの直線BA, AC から作られる角のため、 ∠BAC、∠CABとも書くことができます。
※△ABCは△BCA、△CBAと表しても大丈夫です。
【合同】
形や大きさがまったく同じ図形同士の関係を合同といいます。
2つの三角形が合同かどうかを証明するには、三角形の合同条件が必要になります。
合同は、「≡」という記号を使って表します。
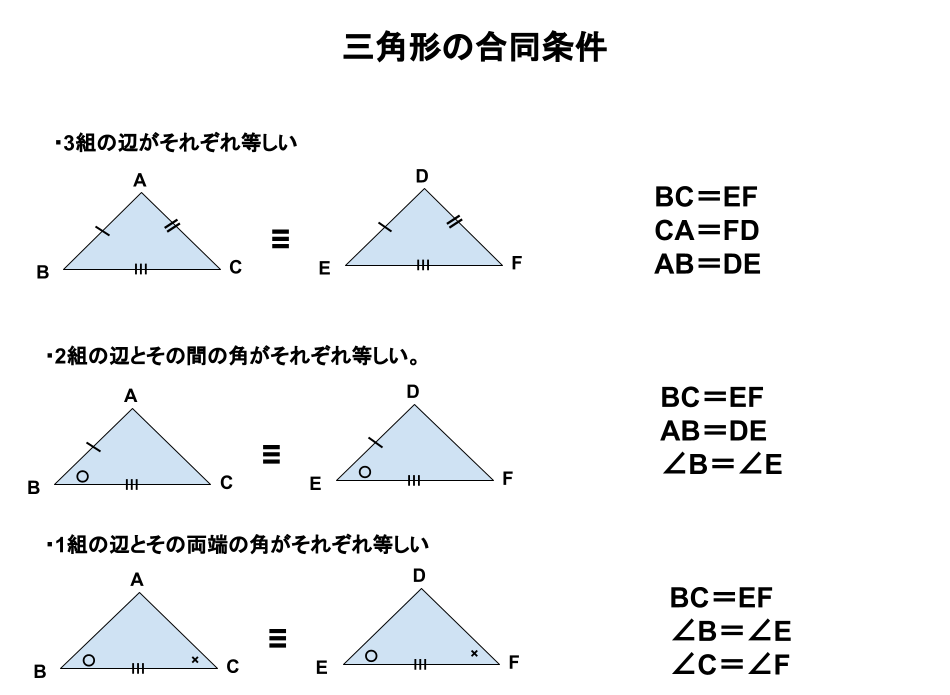
三角形の合同条件は次の3つになります。
・3組の辺がそれぞれ等しい。
・2組の辺とその間の角がそれぞれ等しい。
・1組の辺とその両端の角がそれぞれ等しい。
これら3つの条件のうち1つでもあてはまれば、2つの三角形は合同といえます!
【三角形の成立条件】
三角形を成立させる条件について解説します。
解説①
三角形は2つの辺の長さの和は残りの1つの辺の長さより大きいという特徴があります。
つまり、三角形の3辺の長さを a,b,c とするとき、次の三つの不等式が成り立ちます。
a < b+c
b < a+c
c < a+b
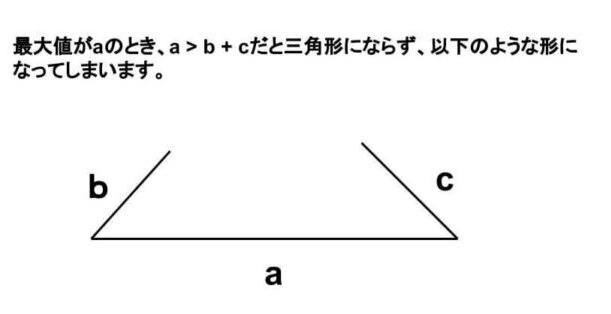
覚えておくポイントは、『△ABCにおいて最大辺がaのとき a < b + c 』になるという事です!
( a > b + cだと三角形として成り立ちません。)
(例題)
a=6,b=3, c=5の三角形の三角形が成立するかを求める場合、最大辺がaのとき a < b + cの三角形の成立条件に当てはめてみましょう!
最も長い辺は a=6
他の 2 辺の和は b+c=8
a < b + c となるので、この三角形は成立します。
答え 三角形は成立する
解説②
2つの辺の長さの和は残りの1つの辺の長さより大きいため、a< b+cになりますが、2つの辺の長さの差は残りの1つの辺の長さより短いとも言えるため、b−c<a、c−b<aが成立します。
つまり、|b−c| < a < b + c と置き換える事ができるのです。
これを覚えておくと以下の問題を簡単に求めることができます!
(例題)
三辺の長さが 3,9,x である三角形を作る場合、 x の範囲を求めよ。
|b−c| < a < b + c に当てはめてみましょう。
|3−9| < x <3 + 9
6 < x < 12 と求める事が出来ます。
答え 6 < x < 12
【三角形の辺の長さと角の大小関係】
三角形の辺の大小関係は、その向かい合う角の大小関係と一致するという特徴があります。
・大きい辺に向かい合う角は小さい辺に向かい合う角より大きい
・大きい角に向かい合う辺は小さい角に向かい合う辺より大きい
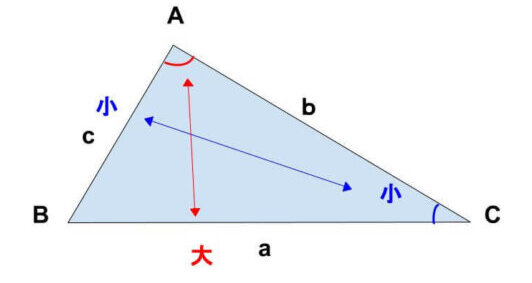
覚えておくポイントは、△ABCは ∠A > ∠B > ∠C の場合、辺の大きさは a > b > C が成立するという事です!
(例題)
△ABC において、a=7,b=4,c=5 の場合、3つの角の大小関係を求めよ
まず、3つの辺の大小関係は、a > c > b という事が分かります。
三角形の辺とその対角の大小関係は一致するので、角の大小関係は∠A >∠C >∠B になります!
答え ∠A >∠C >∠B
【三角形の角度の定理】
三角形の内角について解説します。
・0°より大きく90°より小さい角を鋭角といいます。鋭角三角形はすべての内角が 90° 未満です。
・90°の角を直角といいます。直角三角形は 90°の内角が1つあります。
・90°より大きく180°より小さい角を鈍角といいます。鈍角三角形は90°より大きい内角が1つあります。
すべての三角形の内角の和は必ず 180° になります。
つまり、90度以上の角が2つになることはありません。
これらを知っておくと以下の問題の解答を求めることができます。
(例題)
3つの内角のうち、2つの内角が52°,38°である三角形は、 鋭角三角形・直角三角形・鈍角三角形のどれでしょう?
まずは残りの1つの角度を求めます。
すべての三角形の内角の和は180°のため、残りの角度は以下の計算で求めることができます。
180° -( 52° + 38° )
= 180° – 90°
= 90°
残りの一つの角度は90°です。90°の内角があるのは直角三角形のみになります。
答え 直角三角形
【三角形のさまざまな種類】
三角形には様々な種類があります。定理と合わせてご紹介します。
《正三角形》
正三角形とは3辺の長さがすべて同じの三角形です。
また、3つの内角も同じため、内角はすべて60°になります。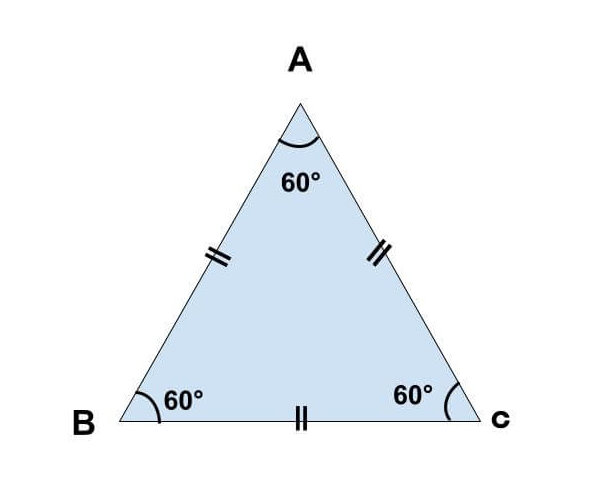
《二等辺三角形》
二等辺三角形とは2つの辺の長さが同じ三角形です。
長さが同じ2つの辺を等辺、残りの1つの辺を底辺、2つの等辺にはさまれた角を頂角といい、残りの2つの内角を底角といいます。
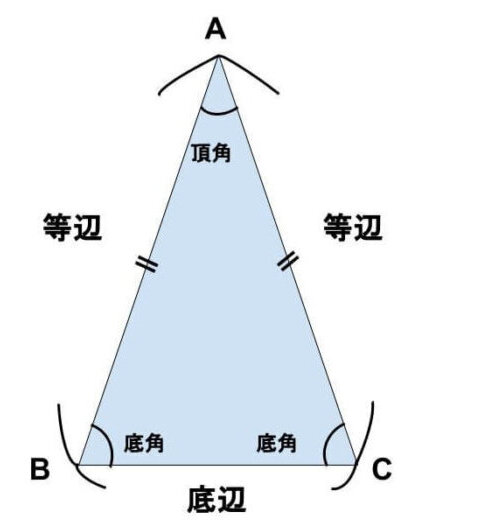
二等辺三角形の性質は以下の2つになります。
①2つの底角は等しい
②二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する
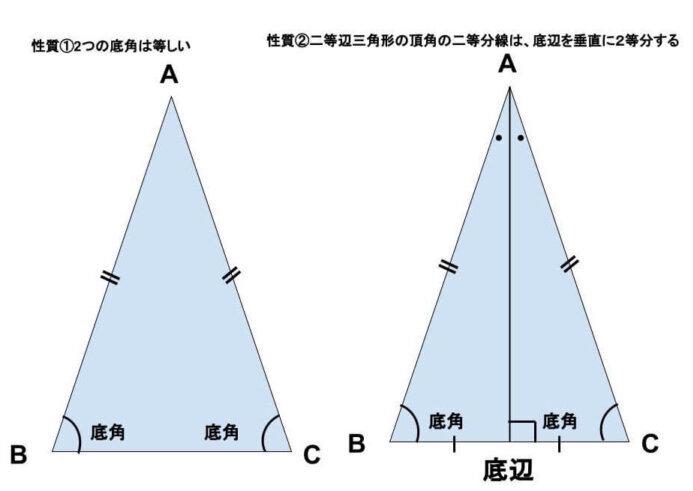
次に二等辺三角形と直角三角形の特徴を持つ《直角二等辺三角形》をご紹介しましょう。
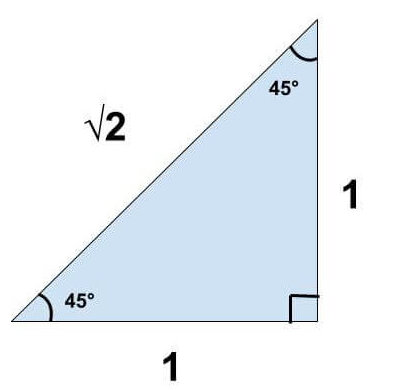
直角二等辺三角形は、長さが同じ2つの辺があり、2つの角度が45°、残りの1つの角度が90°の三角形です。
三角比は底辺:高さ:斜辺=1:1:√2になります。
二等辺三角形の三角比は辺の長さを求めるために必要となるためしっかりと覚えておきましょう!
(例題)
直角二等辺三角形の底辺の長さが4、斜辺の長さを求める場合
直角二等辺三角形の三角比は底辺:高さ:斜辺=1:1:√2 となるため、斜辺の長さは残りの辺の長さに√2をかければ求めることができます。
4 × √2 = 4√2
答え 4√2
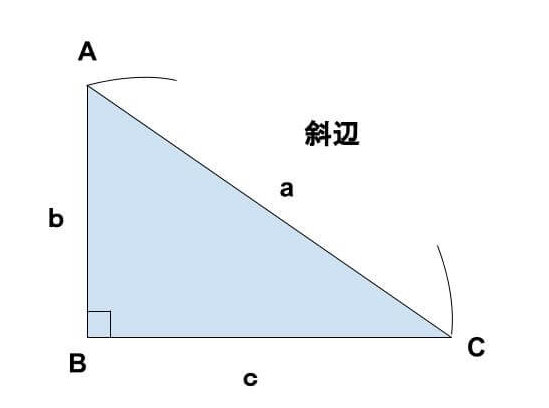
《直角三角形》
直角三角形とは3つの内角のうち、1つの角が直角、残りの2つ鋭角の三角形です。
直角に向かい合う斜辺をa、高さをb、底辺をcとすると、直角三角形の3辺の長さは a² = b² + c² が成り立ちます。
これを三平方の定理(ピタゴラスの定理)といいます。
(例題)
高さ4、底辺の長さ3の直角三角形の斜辺の長さを求める場合、三平方の定理を利用して求めることができます。
三平方の定理 a² = b² + c² に当てはめてみましょう。
a² = 16 + 9
a² = 25
a = 5
答え 5
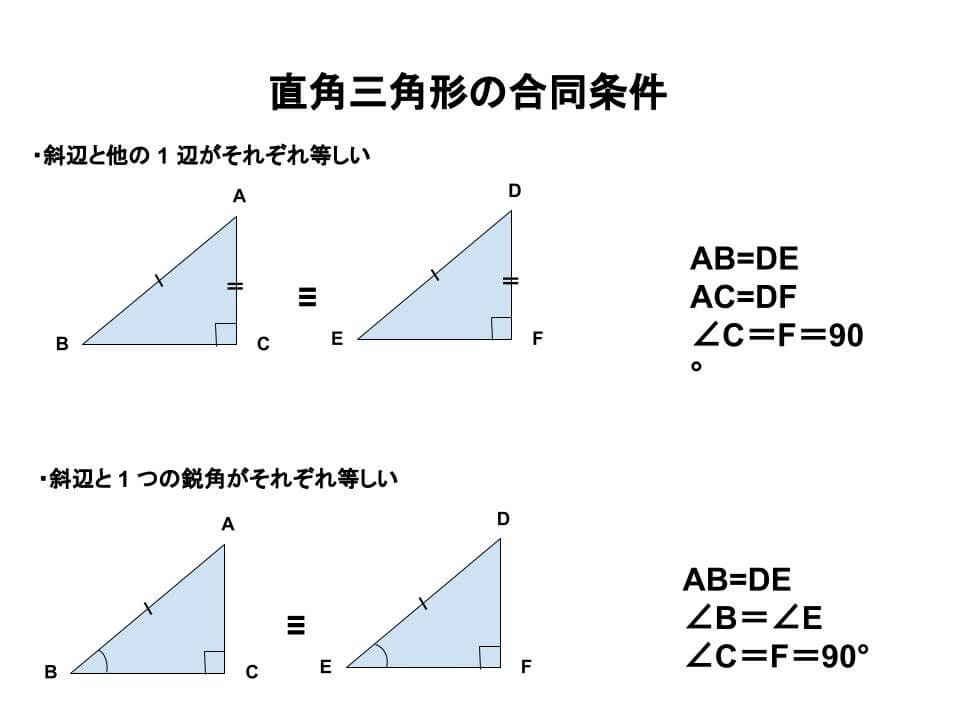
直角三角形の合同の証明には、三角形の合同条件とは別に直角三角形だけに当てはまる合同条件があります。
それは次の2つになります。
・斜辺と他の1辺がそれぞれ等しい
・斜辺と1つの鋭角がそれぞれ等しい
これらの2つの条件のうち1つでもあてはまれば、2つの直角三角形は合同といえます。
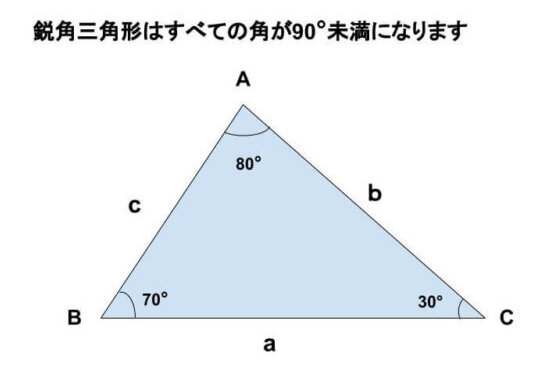
《鋭角三角形》
鋭角三角形とは3つの角度がすべて鋭角の三角形です。
一番大きい辺ををaとすると、鋭角三角形は a² < b² + c²の関係が成り立ちます。
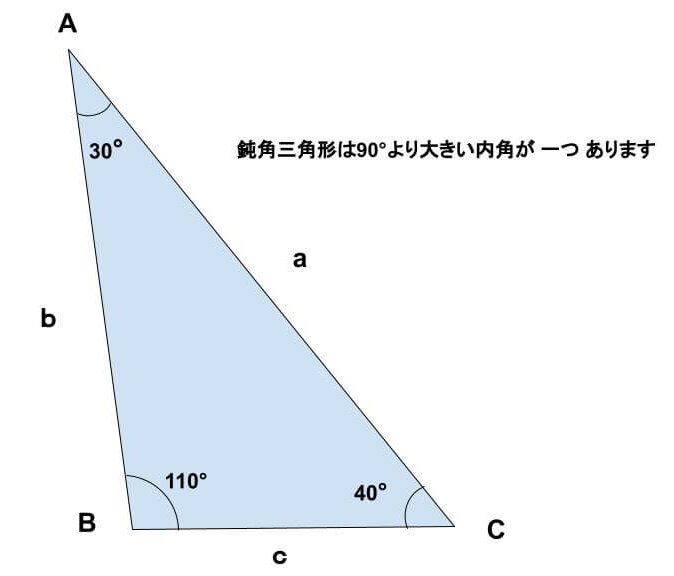
《鈍角三角形》
鈍角三角形とは 内角の1つが鈍角の三角形です。
一番大きい辺ををaとすると鈍角三角形は a² > b² + c² の関係が成り立ちます。
◇まとめ◇
ここまで三角形の種類と定理などを簡単にご紹介しましたがいかがでしたか?
これらを理解しておくと証明問題や計算問題が解きやすくなります。
もっと三角形の理解を深めたい方は、ぜひ個別指導WAMに気軽にご相談ください。
お待ちしております!(^^)!













