こんにちは!個別指導WAMです(^^)
今回は、【円柱とは?体積や表面積の公式を使った求め方】についてお話します。
皆さんは図形問題に苦手意識はありませんか?
授業で公式を説明してもらったけど、よく分からない。
そんな人もいるのではないでしょうか?
ここでは円柱の体積や表面積を求める公式について紹介していきまので、ぜひ最後まで読んでみてください!
Contents [hide]
円柱とは?円錐や角柱との違い
まず円柱について説明していきます。
円柱とは、底が円の形をしている筒状の立体のことです。底面となる2つの円は同じ形をしており、平行になっています。展開すると、同じ形の円が2つと四角形1つになります。

円錐とは、底が円の形をした錘状にとがった形をした立体です。円柱とは異なり、底面が1つしかありません。円柱と円錐を真上から見ると同じ円形に見えますが、真横から見ると円錐は三角形に見えるのが特徴です。展開すると、円と扇形が1つずつになります。

角柱とは、同じ多角形を底面とした柱体のことを指し、2つの底面は同じ形をしており平行です。底面が三角形なら三角柱、四角形なら四角柱となります。

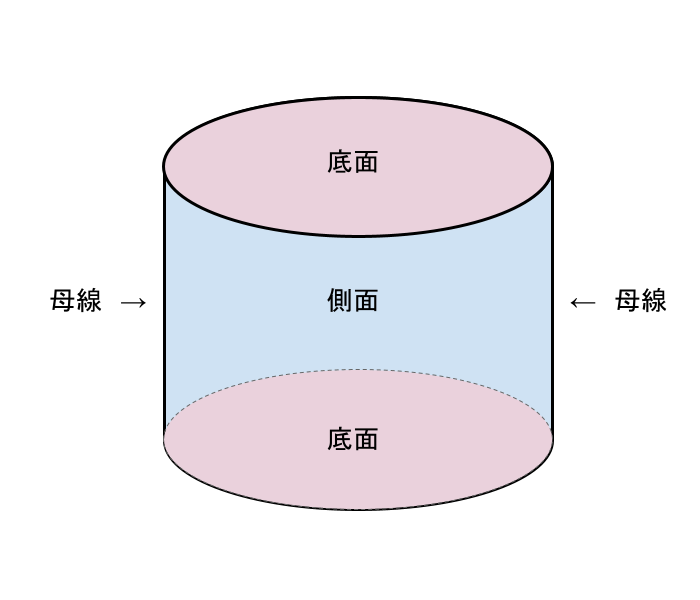
底面とは、上でも少し触れましたが円柱や角柱の上下の面ことを指し、円柱と角柱では上下2つ、円錐では下のみとなっています。底面が2つの場合は、2つの底面は同じ形をしており平行です。側面とは底面以外のまわりの面を指します。母線は立体図形の側面をつくる線のことで、円柱や角柱の母線の長さはそれらの図形の高さに等しく、円錐では展開してできる扇形の半径に等しくなります。
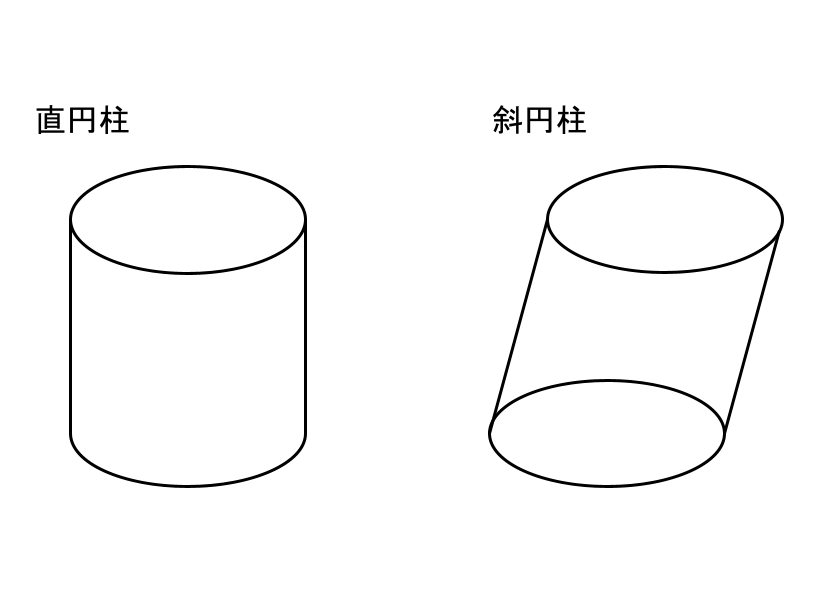
円柱には直円柱と斜円柱があり、母線が底面に垂直な円柱を直円柱といい、そうでない円柱を斜円柱といいます。
公式を使って円柱の体積を求める
それでは、円柱の体積の求める公式を説明していきましょう。
円柱の体積(V)=πr²h→円柱の体積(V)=底面の円の面積(πr²)×高さ(h)→底面の円の面積=半径(r)×半径(r)×円周率(π) となります。
もっと詳しく見ていきましょう。
円柱の体積は、底面積×高さ で求めることができます。
円柱の底面は円の形をしているので、円の半径をrとします。そうすると底面積は、半径×半径×π となるので、r×r×π=πr² となります。
この時の円柱の高さをhとすると、円柱の体積は、底面積×高さなので、πr²×h=πr²h となりますね!
☆簡単な数字を入れて計算してみましょう。
底面の円の半径を3㎝、円柱の高さを10㎝とすると、この円柱の体積は
V=3×3×π×10=90π となります。
このように公式を知っておくと、簡単に体積を求めることができますね!
公式を使って円柱の表面積を求める
次は、円柱の表面積を求める公式を見ていきましょう。
円柱の表面積=2πr²+2πrh となります。
円柱の表面積を求めるには、展開図にして考える必要があります。円柱を展開図にすると、同じ形の円が2つと四角形が1つになりますね。つまり、「底面の円の面積2つ」と「側面の四角形の面積」を足すことで円柱の表面積を求めることができます。
もっと詳しく説明していきます。
円柱の底面は円の形をしているので、円の半径をrとします。そうすると底面積は、半径×半径×π となるので、r×r×π=πr² となり底面は2つあるので、πr²×2=2πr² となります。
底面の円周と側面の四角形の横の長さが等しいことから、側面の四角形の面積は、底面の円周×高さ で求めることができます。
底面の円周=直径(2r)×円周率(π)なので、2πr となります。
この時の円柱の高さをhとすると、側面の四角形の表面積は、2πr×h=2πrh と求められます。
よって円柱の表面積=底面の円の面積×2+側面の四角形の面積=2πr2+2πrh となり公式と同じになりましたね!
☆簡単な数字を入れて計算してみましょう。
底面の円の半径を3㎝、円柱の高さが10㎝とすると、この円柱の表面積は
円柱の表面積=2×π×3×3+2×π×3×10=18π+60π=78π となります。
円柱の表面積も、公式を覚えておくと簡単に求めることができますね!
公式を使わずに円柱の表面積を求める
1.2つ分の底面積を求める
もし公式を忘れてしまっても、円柱を展開すると計算手順が見えてきますね。上でも説明しましたが、円柱を展開図にすると、同じ形の円が2つと1つの四角形になるので、「底面の円の面積2つ」と「側面の四角形の面積」をそれぞれ計算し、足すことで円柱の表面積を求めることができます。
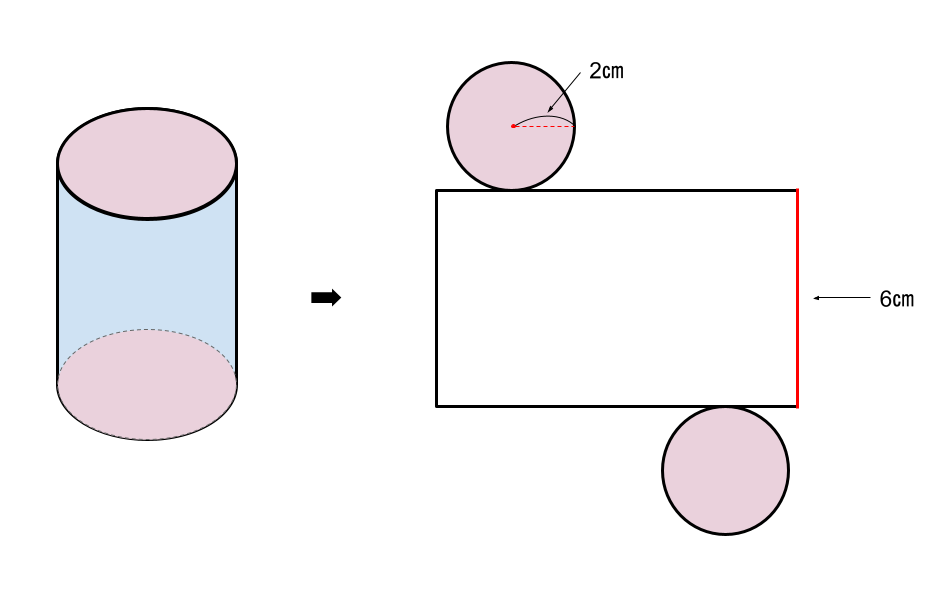
まずは、底面(ピンク)の面積から求めていきましょう。半径2㎝の円の面積は、半径×半径×πなので
2×2×π=4π …①
2.側面の四角形の面積を求める
次に、側面の四角形の面積を求めます。
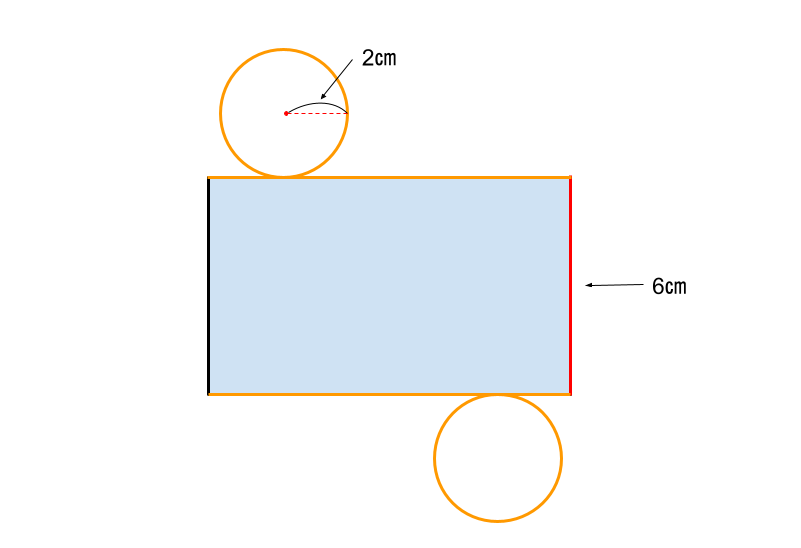
底面の円周と側面の四角形の横の線(オレンジ色の線)長さが等しいことから、底面の円周を出していきましょう。
円周は、直径×円周率なので、円の直径4㎝×π=4π となり、四角形の横の長さが4πと分かりましたね。

すると、四角形の縦の長さが6㎝、横の長さが4πとなるので
四角形の表面積=6×4π=24π …②
3.2つの底面積と側面積を足す
底面積①と側面積②をそれぞれ求めることができたので、最後は2つの面積を足すことで円柱の表面積となります。
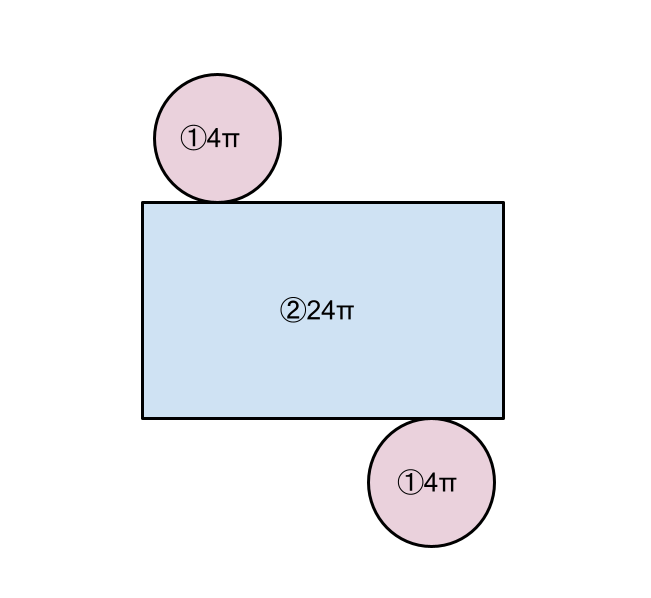
表面積=底面積①×2+側面積②=4π×2+24π=32π と求めることができます。
上のような考え方をすると、公式を使わなくても簡単に表面積を求めることができます!
円柱に関連する公式
・円錐の求め方(公式)
円錐の表面積=πr(L+r)→円周率×底面の半径×(母線の長さ+底面の半径)
円錐の体積=1/3Sh→1/3×底面積×高さ
詳しい説明は下記のリンクから確認してみてください!円錐について説明しています!
【円錐の表面積の求め方は簡単?公式を覚えて練習問題を解いてみよう】
まとめ
ここまで、円柱の体積と表面積について説明してきましたが、いかがでしたか?
公式を理解できると、問題も解きやすくなりますね!
もっと円柱の体積や表面積について勉強してみたい!という方は、ぜひ一度個別指導WAMにお問い合わせください。













