こんにちは!個別指導WAMです(^^)
皆さんは数学に苦手意識はありませんか?
特に、図形に苦手意識を持っている人は多いのではないでしょうか。
さまざまな図形がありますが、ここでは円錐の表面積や体積の求め方について紹介していきます。
ぜひ最後まで読んでみてください!
Contents [hide]
円錐の表面積を求める公式
まず、円錐の表面積を求める公式を説明していきましょう。
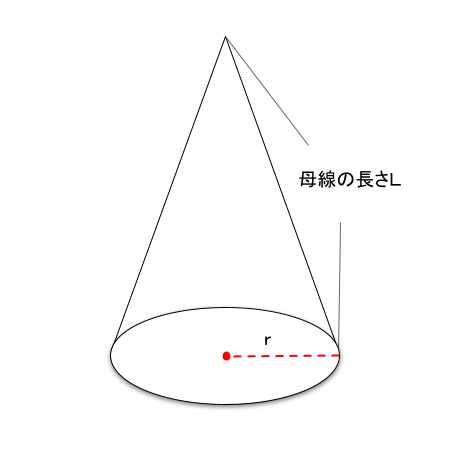
円錐の表面積 = πr( L + r ) → 円周率 × 底面の半径 × (母線の長さ + 底面の半径) となります。
上の図のように、底面の半径がr、母線の長さをLとして表しています。あとは長さを入れて計算するだけなので、公式を知っておくと簡単に円錐の表面積を求めることができます。
表面積の公式を詳しく説明するために、円錐を展開図にして考えていきましょう。

・底面は、半径rの円
・側面を展開すると半径Lの扇形になる
・底面の円周と、扇形の弧の長さが等しい
・半径の長さが等しい扇形の面積は、弧の長さに比例する
〈底面積〉
半径 × 半径 × π で求めることができるので、r × r × π = πr² …①
〈扇形の面積〉
扇形の弧の長さと底面の円周が等しいことから
底面の円周は、直径 × π で求めることができるので、2 × r × π = 2πr となります。
半径の長さが等しい扇形の面積は、弧の長にさ比例しているので
半径Lの円周は、直径 × π になるので、2L × π = 2πL となり
面積は、半径×半径× πで求められるので、L × L × π = πL² です。
この時、弧の長さが2πrとなる扇形の面積を求めればよいので、半径Lの円の面積に、円周に対する弧の長さの割合をかけることで求めることができます。
つまり、扇形の面積 = πL² × 2πr/ 2πL = πLr …② となります。
《円錐の表面積》
底面積①と側面積②を足すと
πr² + πrL = πr( L + r ) という公式ができあがります!
円錐の表面積を公式を使わずに解く方法
試験中、緊張や焦りで公式を忘れてしまうなんてハプニングも起こることがありますよね?
そんな時は、公式を使わずに解く方法も合わせて覚えておくと、とっさの時に役に立ちます!
公式を使わない方法では、円錐を展開図にして考えます。展開すると、半径rの円と半径Lの扇形の2つにわけられます。
それぞれの面積をわけて求めると解きやすくなります!3つのステップに分けて考えていきましょう。
1.底面の円周を求める
まずは、底面の円周を計算してみましょう。
円周の求め方は、直径 × π(円周率)で求められます。
円の半径を3㎝とすると、直径は3 + 3 = 6㎝( 3 × 2 = 6㎝ )になるので、円周 = 6 × π = 6π となりますね。
2.扇型の中心角を求める
次に、扇形の中心角を求めましょう。
「底面である円周の長さ」と「側面である扇形の弧の長さ」が等しいということを方程式にすることで求めることができます!
扇形の半径(母線の長さ)を5㎝、つまり直径10㎝、中心角をαとして計算してみます。
扇形の面積の求め方は、直径 × π(円周率) × α/360 です。
つまり、10 × π × α/360 が、上で求めた底面である円周の長さ6πとイコールになるので
10 × π × α/360 = 6π という方程式ができあがります。
この方程式をαについて解くと、α = 216となり、扇形の中心角が216°と分かります。
3.底面積と側面積を足す
扇形の中心角が求められたところで、底面積と側面積をそれぞれ計算していきましょう。
底面積(円の面積)は、半径 × 半径 × π(円周率)で求められ
底面積 = 3 × 3 × π = 9π となります。
側面積(扇形の面積)は、半径 × 半径 × π × 中心角/360で求められ
側面積 = 5 × 5 × π × 216/360 = 15π となります。
円錐の表面積は、底面積+側面積で求められるので
円錐の表面積 = 9π + 15π = 24π という手順で求めることができます!
しかし公式を使うより時間がかかってしまうので、公式はきっちり覚えておく方が効率的ですね!
円錐の体積を求める公式
次に、円錐の体積を求める公式を説明していきましょう。
円錐の体積 = 1/3Sh → 1/3 × 底面積 × 高さ で求めることができます。
円柱の体積が、底面積 × 高さ で求めることができ、円錐は円柱の体積の1/3ということになります。
なぜ円柱の1/3?と疑問に思っている人もいるのではないでしょうか。
1/3の説明には立方体を使うと分かりやすいです。
1辺が6㎝の立方体で考えてみましょう。
立方体の体積は、底面積 × 高さ = 6 × 6 × 6 = 216㎤ となります。
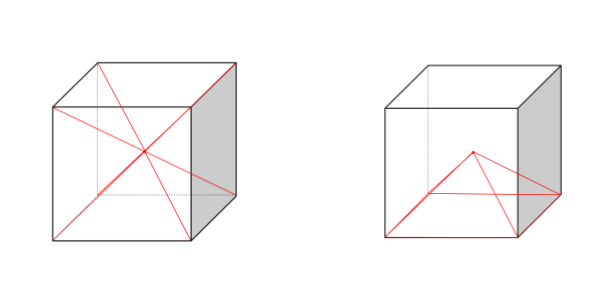
立方体の中心に点を打ち、その点から各頂点に線を引くと、同じ形をした四角錐(ピラミッド)が6つできあがります。
立方体の中に、全く同じ形の6つの四角錐が入っていることがわかりますね!
ということは、四角錐1つの体積は、立方体の体積216㎤の1/6の大きさなので
216 × 1/6 = 36㎤ となります。
ここから方程式を考えてみましょう。
四角錐の底面積は、6 × 6 = 36㎠ となります。
高さは立方体の半分になるので、6 × 1/2 = 3㎝
36 × 3 × x = 36 という方程式を作ることができ、この方程式をxについて解くと
x = 1/3 ということになります。
この1/3が、皆さんが疑問に思う錐の体積を求める公式に出てくる数字なのです!
円錐に関連する公式
・円柱の求め方(公式)
円柱の体積(V) = πr²h → 底面の円の面積(πr²) × 高さ(h)
円柱の表面積 = 2πr² + 2πrh → 底面の円の面積(πr²) × 2 + 側面の四角形の面積(2πrh)
詳しい説明は下記のリンクから確認してみてください!円柱について説明しています!
まとめ
ここまで、円錐の表面積と体積について説明してきましたが、いかがでしたか?
公式を理解できると、問題も解きやすくなりますよね!
もっと円錐の表面積や体積について理解を深めるなら、ぜひ個別指導WAMに気軽にご相談ください。