こんにちは!個別指導WAMです(^^)/
今回は【線対称な図形とは?点対称との違いやポイント】について解説したいと思います。
皆さんは図形問題に苦手意識はありませんか?
「線対称と点対称って似ているけど何が違うの?」と思っている人もいるのではないでしょうか。
ここでは線対称について点対称と比較しながら説明し、線対称の代表的な図形も紹介していきます。
ぜひこの記事を読んでそれぞれの特徴や違いを理解して、少しでも苦手意識を減らしましょう。
線対称とは
線対称とは
まず線対称とは、どのような図形のことを指すのでしょうか。
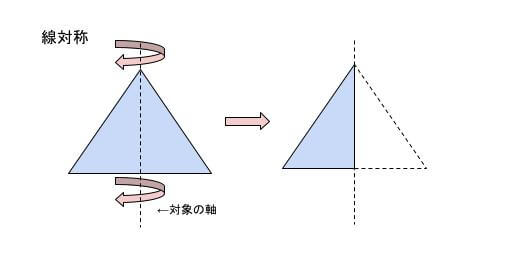
線対称とは、1本の直線を折り目にして折ったときに、折り目の両側がぴったりと重なる図形のことを指します。まるで鏡に反射させた感じですね!この時、折り目にした直線を「対象の軸」、互いに重なる2つの点を「対応する点」、互いに重なる2つの辺を「対応する辺」、互いに重なる2つの角を「対応する角」といいます。線対称は、平面図形を特徴づける性質の一つとなっています。「対象の軸」は、図形によって本数が変わります!
線対称の代表的な図形は、円や正n角形、二等辺三角形、長方形、ひし形などさまざまです。立体の図形であげると、球や正四面体、立方体などです。身近なアルファベットで例えると、AやB、M、Uなどがありますね!
線対称と点対称の違い
次に点対称について説明します。点対称は線対称と似ているので間違えやすい人が多いのではないでしょうか。
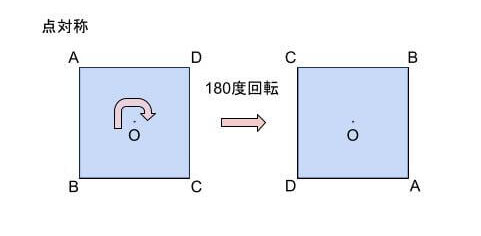
点対称とは、ある1点を中心に180度回転させると、もともとの図形にぴったり重なる図形のことを指します。この時、中心となる点を「対象の中心」、線対称と同様に互いに重なる2つの点を「対応する点」、互いに重なる2つの辺を「対応する辺」、互いに重なる2つの角を「対応する角」といいます。線対称に比べると得点に繋がりやすい単元です!
点対称の代表的な図形は、正偶数角形(正方形や正六角形)、円、平行四辺形などがあります。立体の図形では、球や正四面体以外の正多面体などです。こちらもアルファベットで例えると、NやS、Zが当てはまります!
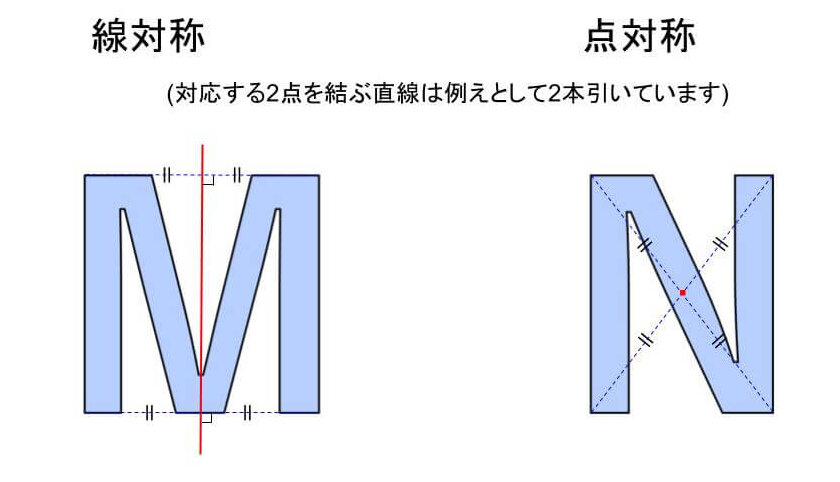
線対称と点対称の性質をそれぞれアルファベットの「M」と「N」を使って見ていきましょう。
線対称な図形の性質
線対称では、「対応する点」を結ぶ直線は、「対象の軸」と垂直に交わります。交わった点から、「対応する点」までの長さは等しくなっています。
点対称な図形の性質
点対称では、「対応する点」を結ぶ直線は、「対象の中心」と通ります。「対象の中心」から「対応する点」、までの長さは等しくなっています。
線対称でもあり、点対称でもあるアルファベットは、「H、I、O、X」の4つです。また、どちらにも当てはまらないアルファベットもあるので、ぜひ探してみてください!
線対称な図形の種類
それでは線対称の図形をいくつか簡単に説明していきましょう!紙などで図形を作成して、実際に線対称なのか確認してみるとより分かりやすいですね。
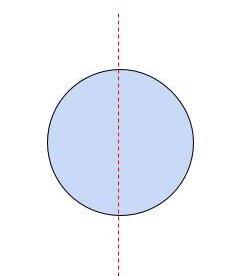
・円形
円形とは、漢字の通りに「まるい形」です。鏡や時計、テーブルなど普段の生活で目にする機会が多いです。円の中心を通るように「対象の軸」を引き、折り返すとぴったり重なります。円の中心を通る直線は全て「対象の軸」になるので、円形では「対象の軸」は無数にあることになりますね!
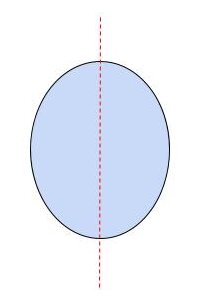
・楕円形
楕円とは、2つの定点からの距離の和が一定となる点の軌跡であり、円を押しつぶしたような形をしています。楕円形の「対象の軸」は楕円のかたちによって、最低でも1本存在します!
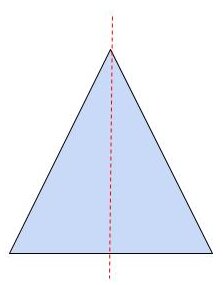
・二等辺三角形
二等辺三角形は、3本ある辺のうち少なくとも2本の辺の長さが等しい三角形です。3本とも同じ長さになると正三角形になります。二等辺三角形の頂点から向かい合う底辺の中心を結ぶ直線が「対象の軸」です。そのため、「対象の軸」は1本だけになりますね!
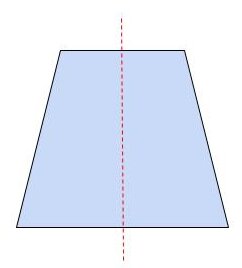
・台形
台形は、少なくとも1組の対になる辺が互いに並行であるような図形で、四角形の一種です。注意が必要なのは、全ての台形が線対称ということではありません。台形のうち、平行ではない辺の長さが等しく、底辺の両端の内角が互いに等しい図形を等脚台形といい、この等脚台形の場合が線対称となります。
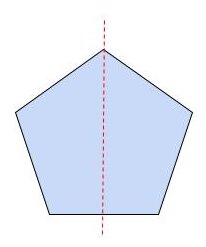
・正n角形
正n角形は全て線対称に当てはまるので、今回は正五角形で説明します。 正五角形は、5つの頂点を持ち、各辺の長さと内角が全て等しくなっています。正五角形での「対象の軸」は全部で5本あります。コンパスと定規を使って正五角形を書いて確かめてみてください!
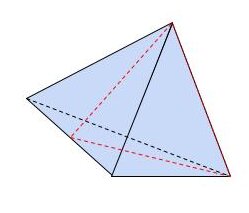
・正四面体
正四面体は、4枚の合同な正三角形を面としている四面体です。補足として、三角形4枚で作る四面体を三角錐といい、正四面体は三角錐の一種となります。「対象の軸」は、頂点から立体の中心を通り面の中央を結ぶ線と、辺の中点と辺の中点を結ぶ線があり、合計で7本となります。
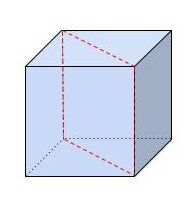
・立方体
立方体(正六面体)とは、空間を6つの合同な正方形で囲んだ立体のことをいいます。サイコロをイメージしてみると分かりやすいですね!「対象の軸」は、頂点と頂点を結ぶパターン、面の中央と面の中央を通るパターン、辺の中点と辺の中点を結ぶパターンに分けることができ、合計13本になります。実際に書いて確かめてみると良いでしょう。
まとめ
ここまで線対称と点対称について説明してきましたが、いかがでしたか?
テスト問題では、線対称の図形と点対称の図形を見分ける問題がよく出ていますね。上で説明したとおりに、それぞれ「対象の軸」と「対象の中心」が必要なので、自分で書き足して見分けられるようになりましょう!
線対称と点対称についてもっと詳しく勉強したいという方は、ぜひ個別指導WAMに気軽にご相談ください。