教室ブログ

2024.09.23

ユークリッドの憂うつ

藤の木校

こんにちは、個別指導Wam藤の木校です。

算数、あるいは数学、好きですか。

「算数（＝小学校の頃）は好きだったけど、数学（＝中学以降）は好きじゃない」とか、「計算がどうも苦手で」とか、学校の勉強の中でもよく苦手教科とされ、勉強イコール算数（数学）イコール嫌なもの／難しいものの代名詞とされているのは、今も昔もあまり変わらないのではないでしょうか。

でも算数／数学は計算だけではありません。小学1年の算数の中心は確かに「数と計算」ですが「図形」もあります。それに小学2年で既に「表とグラフ」が出てきます。だから勉強＝算数＝計算＝嫌い、とは一概に言えないはず、です。

およそ、小学校から高校までの算数／数学は、1）数と計算、２）図形、３）関数、４）確率・統計の大きく四分野に分かれています。学年が上がるに従ってその四分野がそれぞれ難しくなっていくのですが、中学3年の終盤、ある“異変”が起こります。異変とは、１）数と計算と２）図形　の融合、いわゆる「三平方の定理」、またの名を「ピタゴラスの定理」です。高校ではさらに１）数と計算と３）関数　が融合します。そう聞くとますます憂うつになるかもしれませんが、ちょっと楽しみという人もいるかもしれません。どうでしょうか。

中学に入ると文字式が登場し、１）数と計算は代数（だいすう）学、２）図形は幾何（きか）学、３）関数は解析（かいせき）学という別名でも呼ばれ、大学でも引き継がれていきます。別名で呼ぶと何だかカッコイイし、その基礎を学習していると思うと、頑張ろうと思えませんか、いやいや余計に果てしなく思えてやる気なくしますか。

でもこの算数／数学は、はるか昔、紀元前から脈々と引き継がれ、多くの人が学んで検討して研究して、それが発展してきた結果、今の便利な世の中があるのです。その人類の2000年以上をほんの12年（小・中・高）で一気に学ぶことができる、というのも、考えようによっては有難く思えませんか。

その一例をご紹介しましょう。

算数／数学の２）図形は別名「幾何学」と呼ばれると書きましたが、「ユークリッド幾何学」と呼ばれてもいます。なぜ「ユークリッド」が付くのでしょうか、そもそもユークリッドってなに？

ユークリッドとは、紀元前3世紀ごろの数学者エウクレイデス（その英語読みがユークリッド）のことで、それまでの数学、つまり古代ギリシア数学の成果を集めて体系化したことで知られています。じゃあ「それまでの古代ギリシア数学」ってどうだったのでしょう。

古代ギリシア数学のはじめはまず、ギリシア数学の開祖とされるターレスです。聞いたことがないかもしれませんが、ギリシア哲学でも最初に出てくる人で、紀元前624年頃の生まれとされ、三角形の性質を使って実際の海の上にある船の位置を測定したことでも知られています。

ターレスの弟子の一人が、先に出てきた「ピタゴラスの定理」のピタゴラス。紀元前580年頃に生まれ、エジプトで勉強後イタリアに学校を建てたもののそれが宗教団体のようになってしまったのですが、その独特の学問をピタゴラス学派と呼ばれました。

そのピタゴラス学派と交流していたのがプラトン。ソクラテスの弟子（アリストテレスの先生）として哲学史上で有名な人です。

そのプラトンの流れをくむ哲学者や数学者について長い間勉強をしていたのがエウクレイデス（ユークリッド）です。

さらにユークリッドの弟子に教えを受けたのがアルキメデス（紀元前287年生まれ）です。

ターレスからユークリッドまでおよそ300年。今年2024年の300年前といえば1724年、なんとまだ江戸時代です！「それまでの数学の成果を集めて体系化」って言ってもすごく長いんですね！　また古代ギリシアといっても、エジプトからシリア、イタリアまでなにげに広範囲であることがわかります。

その300年かけて培われた数学を、ユークリッドが体系化し編纂した本が、数学書「原論」（英語名「エレメンツ」）です。今でいう教科書で、「世界で聖書の次に読まれた本」として知られています。

「原論」がこれほど読まれた理由は次の通りです。（「幾何学の父、ユークリッドの功績と生涯、原論について」より引用）

ー　ー　ー　ー　ー　ー　ー　ー　ー　ー

原論のスゴさは数学の「公理（こうり）」というものを明確に定めたことにあります。

聞き慣れない言葉かと思いますが、簡単にいうと「論理の前提」です。数学の特徴は論理を積み重ねて、様々な定理や公式を発見していくことです。ですが、どれだけ厳密な理論を積み重ねても、一番最初の土台が間違っていれば、その理論は意味がありませんよね。現代の数学という学問を1本の木に例えるなら、「定理」が葉っぱ、「定義」が木、「公理」が土みたいなイメージです。土がしっかりしているから、木が元気に育ち、木が育つから緑が生まれます。それと同じで数学は、厳密な「公理」を決め、「定義」をしているから、いろんな定理が生まれるし、その定理を信頼することができるのです。しかし、当時はそのような考えを持つ者はいませんでした。そんな中、ユークリッドは数学の論理においても、確固たる土台が必要だと気づいたのですね。この数学の土台を固めたのが原論なのです。

ー　ー　ー　ー　ー　ー　ー　ー　ー　ー

まとめると次のようになります。

「公理」：ある理論の出発点となる仮定

「定義」：ある概念の内容やある言葉の意味を他の概念や言葉と区別できるように明確に限定されたもの

「定理」：定義や公理から証明することができるもの

「定理」は、定義と既に証明された別の定理を用いて証明することができるのですが、「公理」は「証明できないけれど、正しいと仮定して論理の出発点におくもの」になります。

言い換えるとこうです。ある定理に対して「なんで？」「なんで？」と繰り返していくと必ず公理が出てきます。この公理に「なんで？」と質問しても、「それは説明できないけど、誰が考えても当たり前だから正しいと考えているんだ」としか言えないのです。

公理と定義をもとにして、様々な証明をしていき、それがいつしか大きな樹木のようになっていく。中学2年以降に習う図形の証明問題がまさにそうで、図にするとこのようなイメージです。

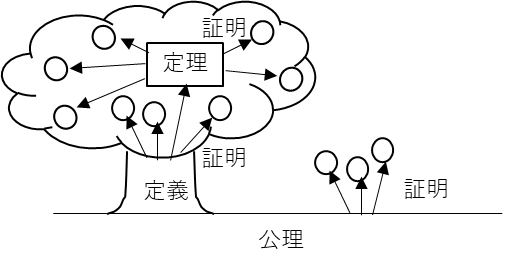
＜公理・定義・定理のイメージ＞

例えば「ピタゴラスの定理」は、公理である「異なる2点を通る直線を引くことができる」や、定義である「三角形とは一直線上にない三点を結ぶ図形である」をもとにして、定理である「直角と隣り合う2辺の長さがそれぞれa、b、斜辺の長さがcとなる直角三角形ではaの二乗＋bの二乗＝cの二乗」が証明される、となります。もちろんその定理をもとにさらに様々な証明や定理が成立していくことになっているのです。

とはいえ「原論」は「数学の集大成」ですから、幾何学だけでなく当時の様々な理論が含まれていました。しかし19世紀になって公理の一つが疑問視され、それまでの幾何学を見直して「非ユークリッド幾何学」が新たに生まれることになりました。

でも疑問視されたのは「平面以外に適用するとおかしなことになる」という点だけだったので、裏返すと平面に限ってはこれまでの理論が使えます。そのため、それまでの幾何学は「ユークリッド幾何学」と呼ばれるようになり、それを私たちは小・中・高と学んでいるわけです。

ちなみに計算や代数学はインドの方が天才的でしたので、ユークリッド幾何学は当時世界で最も優れていたと言えるでしょう。

どうですか、これが12年間で学べるなんて、少しありがたく思えませんか。

ユークリッドのエピソードの中にこのようなものがあります。

ある青年が、ユークリッドについて幾何学を習いはじめました。ところがしばらくしてこの青年はユークリッドにききました。

「先生！　こんな難しいことを勉強して何の得があるのですか」

と。これを聞いたユークリッドは、さっそく下男（今でいう事務員）を呼んでいいつけました。

「この人に三ペンスおやり。この人は、学問をしたらすぐ得をしなければならないと思っているようだから」

と。

中学2年以降であれば、数学の図形で悩んでいるかと思います。でも2000年以上前の人も、同じように悩んでいたということですね。皆さんも、勉強が難しくなってくると「勉強して何の得になるんだろう」と一度ならずとも呟いたことがあると思います。

でも、いくらかもらえば勉強をあきらめるべき、とはなりませんよね。ユークリッドは怒っていたのです、学問に王道なし、千里の道も一歩から、と。途中で音（ね）を上げる人がいることにユークリッドは憂うつだったに違いありません。