教室ブログ
皆さんこんにちは。WAM黒原校の米井（こめい）です。
なにやら、ノーベル賞学者としても有名な天才物理学者・数学者のロジャー・ペンローズが、1970年代から半世紀にわたって探し求めてきた「ある図形」が話題になってるそうです。
なんでも、およそ50年もの間、数学者をはじめとする幾多の人たちが探究し続けてきたこの「ある図形」が、ついに発見されたっちゅうんで大騒ぎらしいです。
その名は「アインシュタイン・タイル」。
ん？アインシュタイン・タイルってナンゾ・・・？？
全くピンとこないですよね！
そんなあなたにざっくりご説明をば・・・
実は数学の世界には、「平面を隙間も重なりもなく敷き詰める図形」を探究する「平面充填（じゅうてん）」とよばれる分野が存在しちょります。
正方形や正三角形を使えば、ごく簡単に平面を敷き詰めることができるのは大体おわかりかとは思いますが、数学的に興味深いのは、「非周期的」とよばれる複雑な平面充填なんだわさ。
多くの数学者たちが、この非周期的な平面充填に魅了され、「それだけを可能にするのはどんな図形か」、そして「いかに少ない種類の図形でそのようなことが可能か」ってな具合に追い求めてきたってんだから全く驚きだべぇ。（決して暇人なわけじゃぁないですからね！）
ざっくり言うと、「一見いびつな形してるのに、何枚も重ねたら綺麗にかみ合って平面を作ることができる、なんとも不思議なパズルのピース」みたいなイメージです。
非周期的な平面充填だけを可能にする図形が初めて確認されたのは1964年のことで、じつに2万426種類の図形によって、平面が敷き詰められてたってんだから驚きですわなぁ。
しかもこの膨大な数を減らす試みはその後の10年間で一気に進展し、1974年にはなんと2種類の図形で可能なことにまでたどり着いたっちゅうんだから、すごいですよねぇ。（イヤもうほんま凄い凄すぎる）
その発見者の名前はロジャー・ペンローズって方なんで「ペンローズタイル」らしいです。
↓こんなやつ↓
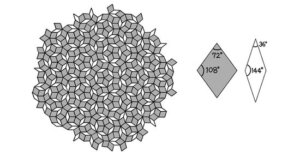
よぉーーくみると、確かに色付きの太目のひし形と白抜きの細長いひし形の2種類のタイルだけしか使われていないですよね。
ここまで凄いとちょっと我々凡人にはただただ「ぶっへぇ～」でしかないとですが、簡単なやつであれば平面充填ができる形状はいくつもあります。
たとえば三角形ならば、たとえそれがどんな辺の比率であっても（同じ三角形どうしなら）平面充填が可能です。
理由としては同じ長さの辺どうしを合わせると、向かい合った辺が平行の四角形ができるからです。
向かい合った辺が平行の四角形は、必ず平行な棒状にできますから、深く考えるまでもなく必ず平面充填できます。（平行の平行は当然平行DAYONE！的なノリです）
同様に、任意の四角形も長い辺どうしを合わせると、実は向かい合った辺が平行の六角形ができるので、必ず平面充填になるんです！（狐につままれた感覚みたいですが面白いですよね！！）
↓こんな感じ↓
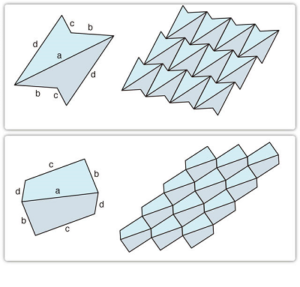
そして、冒頭にあった「アインシュタイン・タイル」というのは、
・繰り返しパターンを作らず
・鏡像なしで
・2次元の表面を無限に敷き詰めることができる
・単一の非周期タイル
ってことなんです。
この辺までくるとこの「アインシュタイン・タイル」がいかにすごいか何となく感じてきた人もいらっしゃるんではないでしょうか。
そして、勘のいいひとなら「え？いびつな形をしたたった一つのパーツで？！不規則に？！平面を敷き詰められる？？そんな図形無理なんぢゃね？？」って感じた人も少なくないはず。
そう！
実はずっとこの「アインシュタイン・タイル」は「存在しない」と考えられてきたんですよね。
なんせ最初に発見された1964年では2万426種類の図形をつかってたのが、たった10年で1974年には2種類にまで絞れたにも関わらず、その1974年を最後に2種類⇒1種類にはずっとできなかったんですから。
そしてそんな「アインシュタイン・タイル」がついに発見されたってので大騒ぎなわけなんですねぇ。
そろそろ皆さんも、非周期モノ・タイルとよばれるこの図形は、いったいどんな形状なのかめっちゃ気になってきたんじゃあ～ないですかぁ～～？
ええそうでしょう！
そうでしょうとも！！
っちゅうわけで、いよいよお見せしましょう。
わたくしめのたわわに実った胸の谷間を！（ﾅﾝﾃﾞﾔﾈﾝ）
イヤ・・・もう最近？いや結構前からか・・・・肥えて肥えてしゃあないんですわ。
とまぁ誰も得しないボケを一つはさんだところで、今度こそお見せしましょう。
↓どやぁ～↓
なんかTシャツみたいなハットみたいなそんな形ですね！
ちなみに「アインシュタイン・タイル」の名前の由来は、ドイツ語で「一つの石」、転じて「1枚のタイル（モノ・タイル）」を意味するein steinに由来してるそうです。
そういうわけで、今回は平面充填界のプリンスこと「アインシュタイン・タイル」についてお届けしてみました。
今まで存在しないと考えられていたものが発見されるのって、ある瞬間を境に今までの常識が非常識にひっくり返ることなので、やっぱりなんだかそれだけで胸がワクワクしちゃいますよね！！
たった一つの発見が、一瞬で世界をガラっと変えるんです！
ちょっと今回真面目なお話でしたが、「常識」というのは、その時代における多くの人が信じている事象に過ぎないので、必ずしも正しいわけでなく、ときに常識は時代とともに変わりゆくものだってことですね。
お子さんの可能性は本当に無限大ですので、例えその時代の常識からはみ出ていたとしても、枠から外れる事をおそれずに自身の可能性を信じてクリエイティブに生きてほしいと願っております。
ご存じの方もいらっしゃるかもですが、数学には全部で7つほどの未解決問題が存在します。
この問題には懸賞金が掛けられており、「ミレニアム懸賞問題」といって解いたら1億円もらえるそうなので、金の亡者であるチャレンジ精神に満ち溢れた素晴らしい方は挑戦してみるのもよいかもですね。
