教室ブログ
こんにちは、個別指導WAM高岡駅南校の四柳です。
今回は、小学生の知識で数学を解いてみましょう!
【問題】
半径5cmの円に内接した正方形が一つあります。この正方形の対角線は、
もちろん円の中心を通ります。この正方形の面積は何㎠でしょうか。
高校生や大学生は、普通に考えれば『三平方の定理』を使って解きますね。
しかし、今回は三平方の定理を習ってないので、高校生も大学生も焦るかも。
皆さんは学校で、正方形の面積は、1辺×1辺(=1辺の2乗)と習って
います。そして、1辺の長さから正方形の面積を計算する問題を、何度も
何度も繰り返してきているので、この公式は定着しています。
でも、それだけではこの問題が解けません。
では、対角線から正方形の面積は解けないのでしょうか。
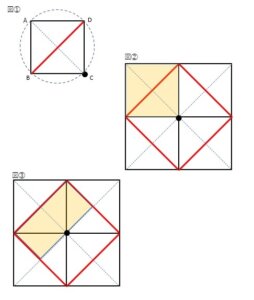
下の図①のように、正方形ABCDがあります。
点Cを中心に時計回りで90度ずつ3回転がすと図②のようになります。
図2の赤線で結ばれた四角形は「正方形」です。
対角線(赤線)を一辺とする正方形に、元の正方形の面積を当てはめると、
赤線の正方形の半分の面積であることがわかります。
つまり、正方形の対角線の長さがわかれば、正方形の面積が計算できる
ことが、この図から判ります。
正方形の面積は、対角線×対角線÷2 でも計算できたのです。
つまり、今回の問題は、10×10÷2 = 50㎠ が答えとなります。
この算出方法は意外と気づいていないかもしれませんね。
数学の図形の問題は、解き方が一つだけではないことが多いです。
この夏、いろんな問題に挑戦してみましょう!
個別指導WAM高岡駅南校
電話076-673-2857