
教室ブログ
川越駅前校です。本日は埼玉県難関私立高校・慶應義塾志木高校の入試についてつづりたいと思います。




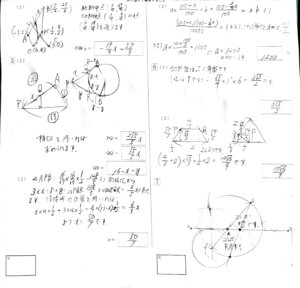
画像が粗くてすみません。
2022年度の入試数学はこんな感じの答案となります。
構成は以下のとおり
1.小問集合(方程式・数と式)
三平方の定理との融合、因数分解と素数がテーマの応用問題です。(1)は大小関係をすべて書き出して考えられるα, βを求めてtへとつなげること、(2)は素数となるとき「素数×1」という関係が浮かべられるかがポイントです。
2.比例と関数
2次関数と図形を絡めた応用問題です。(1)は座標と平行四辺形の面積, (2)は台形の面積2等分線を問うものです。上底・下底をとおる直線の求め方は一般的な公立の中学校において扱わないので、+αの知識が必要です。
3.図形
テーマは傍接円です。(1)はそれぞれの長さを文字式で表せるか, (2)は一方の長さが与えられているときのもう一方の長さはどれだけかという問題です。大問2同様に図も与えられていなければ、内容も一般的な公立中では扱いません。ここでも経験の有無に左右されたことでしょう。
4.資料の活用
立方体の色塗りの場合の数です。(1)6色すべてを使うとき, (2)と(3)は5色を使うときが出題されています。1ヵ所を固定して考えるのですが、高校数学の範囲でこれもまた中学の内容では太刀打ちできません。
5.方程式
値上げと販売個数の増減についての文章題です。難問ぞろいのなか、唯一自信を持って得点できるであろう難度の問題です。割合についてはどんなタイプにも対応できるよう前もって準備しておきたいところです。
6.図形
正八面体の体積2等分問題です。正八面体の性質を知ってさえいれば、どういった面になるのかも見えてくるはずです。正八面体は3つの正方形が見えること, 各面の重心を結ぶと立方体になることなどいろいろと重要な特徴があるので、上位難関校受験を考えている生徒さんはしっかり覚えておきましょう。
7.図形
作図問題です。最短距離の点Rはほぼすべての受験生が習っていることでしょう。一方で、角が2倍となる点Sはひらめきが必要な超難問です。最終問題ということで受験生のほとんどが手をつけていないかできていないと思われます。
県内最難関私立高校だけあってさすがに一筋縄ではいかない問題ばかりですが、先述のとおりどれも経験がものをいう内容でもあります。早めのスタートを切って新しいことをどんどん吸収する積極さを忘れず、勝利をもぎとってください。









