
教室ブログ
こんにちは。Wam種池校の車です。
現在種池校は夏期講習真っ最中の時期なので、どの学年の生徒さんも今までに学んできたことの復習を中心に授業を行っています。
特に中学校3年生の生徒さんたちは、高校受験対策のために真剣に取り組んでくれています。毎日のように授業に来てくれている生徒さんも何人もいます。
数学の復習の授業を行っていて、皆さんがよく覚えている所と忘れがちな所というのは、大体決まっているものです。
特に多くの生徒さんが忘れていることの一つが、今回の記事で取り上げる円錐の側面積の計算方法です。難しいというより、単純に解き方を覚えていないのです。覚えていることさえできれば、あとは数字を当てはめるだけですから。
しかし、そこでただ「覚えておいてね」というだけでは、指導としては不十分なのではないかと考えています。多くの生徒さんが忘れているということは、きっとみんなが記憶に残りにくい覚え方をしているということでしょう。
では下図の円錐の側面積を求める問題を考えてみましょう。底面の半径が4cm、母線の長さが12cmです。
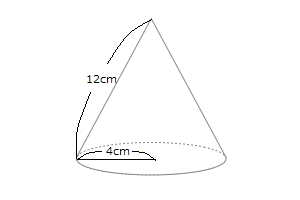
まずは一番真面目でオーソドックスな解き方を説明します。円錐の展開図は下図のような円とおうぎ形となり、側面にあたるのはおうぎ形の方です。
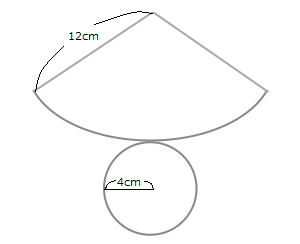
つまり、このおうぎ形の面積を求めればよいということになります。
おうぎ形の面積の公式は、円周率かける半径の2乗かける360分の中心角だから、中心角を求めなければいけなくて、
そのためには弧の長さの公式を使って・・・・・・と、よっぽど解き慣れている人でなければこの時点でうんざりしてきます。
そう、この解き方は「真っ当だけど非常に面倒くさい」のです。もっと楽な解き方があればいいのにと思う人が多いでしょう。
実は、とても楽な解き方が存在します。
円錐の側面積 = 底面の半径 × 母線の長さ × π
という計算式があるのです。
この式は中学校の数学の教科書には載っていませんが、覚えていると非常に簡単に計算をすることができるため、参考書や塾用教材などではしばしば見かけます。
これで円錐の側面積はバッチリだ、と言いたいところですが、実際この計算式を覚えている3年生にはほとんどお目にかかったことがありません。覚えれば解けるというのは間違っていないのですが、ほとんど誰も覚えていないんです。
覚えていないのは単に生徒の勉強不足なのでしょうか?それ以前に、そもそもこの公式は絶対的に頭に入りにくいのではないかと思います。
なぜこれで側面積が計算できるのか全然わからないし、ピンとこないという気持ちは非常によくわかります。
ということで、私は数学の授業を行うとき、この式を覚えさせようとはしません。かといって、最初に紹介した中心角を経由するやり方もおすすめしたくはないです。
面倒くさくなく、なおかつ直感的に頭に入る解き方として、私が最も好むのは以下の方法です。
その名も「おうぎ形って三角形っぽいよね法」です。
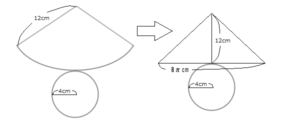
上図のように、おうぎ形をグニャリと変形して、三角形と見て面積を計算します。
三角形の面積は、皆さんご存じ底辺×高さ×(1/2)ですね。
この場合の底辺はおうぎ形の弧の長さにあたるわけですが、これは底面の円周と等しいため、2×4×π=8πcmとなります。
そして高さはおうぎ形の半径、すなわち母線の長さと等しいので12cmです。
すなわち、面積は8π×12×(1/2)=48π㎠となります。
これが計算の手軽さと覚えやすさを兼ね備えた解き方として、個人的には一番良いと思っています。
今まで授業でいろんな生徒さんにこの解き方を教えてきましたが、なかなか良い反応をしてくれることが多いです。
おうぎ形を三角形と見るなんて卑怯だと思われるかもしれませんが、厳密な話をするなら、これは高校数学で学ぶ積分に発展する考え方で、突き詰めればこの考え方によって求められる面積は正確だということがわかります。
円錐の側面積の解き方を覚えていなかった人、覚えてはいたけど面倒くさいと思っていた人は、今日からこの解き方に乗り換えてみませんか。









