
教室ブログ
”分布”と二項分布
記事を読んでいただいている皆様
お世話になっております。
個別指導Wam城北中曽根校の小島です。
最近何かと「分布」に縁があります。
発端は長岡技術科学大学の過去の問題を解いたことでした。
下記のような数学の確率の問題です(問題文は省略・改変してあります)。
「2つの動点が数直線上の原点にあり、一回の試行により、それぞれ別々に1/2の確率で+1または-1動く。
n回試行したとき、2つの動点が同じ座標にある確率を求めなさい。」
すぐに二項分布の問題だと気が付き、分布や誤差の計算に悩まされた大学生時代を思い出しました。
それからというもの「分布」について思いを巡らせていたのですが、昨今のビッグデータの流行があってのことか、高等学校の新学習指導要領で「統計的な推測」がベクトルに代わって数学Bでの履修単元になるという話があり、また、Wamノートで偏差値についての記事を読んでいたこともあり、最近は分布に縁があるなあと思った次第です。
前置きが長くなりましたが、このページでは最近何かと縁がある「分布」について、何か書いてみることにしましょう。
まずは一般的な”分布”というものについて書き、その後で長岡技術科学大学の問題に出てきた二項分布について書いていきます。
そもそも分布とは何でしょうか。
手元にある「三省堂・新明解国語辞典」によれば、分布とは、
「粗密の程度を含めた、空間的な広がり具合。」
のことだそうです。
例えば日本の人口分布を考えてみましょう。
「空間的な広がり具合」ということについて考えてみると、人口は日本列島全域に分布しています。
海の上に住むことは難しいため、逆に言えば海が人口分布の広がりを留める壁の役割を持っています。
人口は日本列島全域に分布していますが、分布は一様ではありません。
暮らしやすい平野部では人口が多くなり、人が暮らしにくい山岳地帯などの場所では分布が少なくなっていたり、人口が0の場所もあります。
これは「粗密の程度を含めた」という部分に関係していて、平野部では人口分布が密になり、人の暮らしにくい場所では人口分布が粗(まばら)になります。
分布とはこのように、どこにどれだけの人がいるか(物があるか)を問題にします。
また、分布を考える上でもう一つ大事な点は、その分布を決めるルールは何かということです。
先程の人口分布では、人が暮らしやすいかどうかが分布を決める一つの要素になっていました。
さて、二項分布の話に入っていきましょう。
具体例を出して説明します。
ここに二枚のカードがあります。

二枚のカードの表面には、それぞれ矢印と星が描かれています。
裏面はどちらも真っ白なので、裏返すと二枚の区別は付きません。
以下のような操作をしてみましょう。
1.点数がゼロからスタートします。
2.二枚のカードを裏返し、どちらがどちらか分からないよう、カードをよくシャッフルします。
3.どちらか一枚を表にします。
4.星が出たら点数に1点追加し、矢印の場合は点数が変わりません。
5.2~4を100回繰り返します。
この操作は、一回の試行で1/2の確率で1点追加し、1/2の確率で点数が変わらないということになります。
最高点は、100回連続で星が出た場合の100点で、最低点は、100回連続で矢印が出た場合の0点となります。
この操作を100人の人に行ってもらい、得点分布のヒストグラムを作ります。
ちなみにヒストグラムというのは、下の画像のようなグラフのことです(このヒストグラムは私がてきとうに数字を決めて作ったものです)。
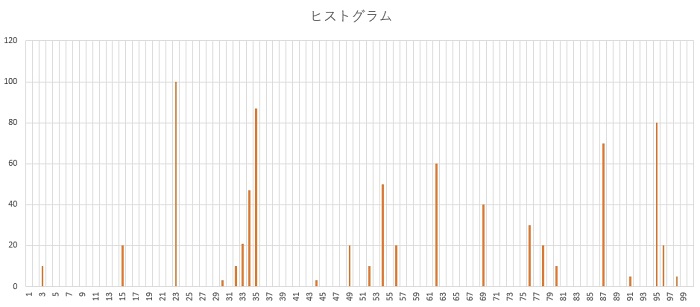
横軸が点数で、縦軸がその点数を取った人数を表しています。
上のヒストグラムを読み取ると、例えば15点取った人数は20人、23点取った人数は100人などということが分かります。
さて、実際の点数の分布はどうなるでしょうか。
想像してみてください。
下の画像がカードめくりのヒストグラムです。
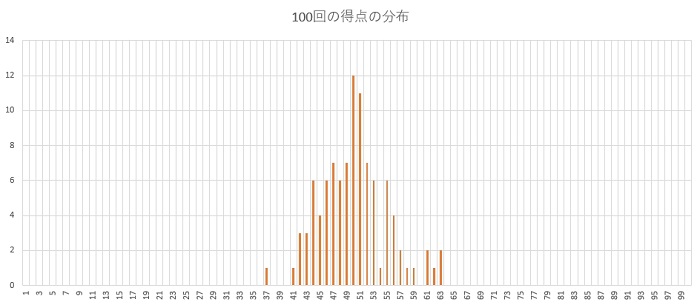
中心の50点近くを中心に、左右に広がる分布になっています。
分布は中心に偏っており、極端に大きい点数・小さい点数を取っている人はいませんでした。
想像は当たったでしょうか?
ちなみにこのグラフは、実際に100人に試行してもらって作ったわけではなく、Excelのマクロでシミュレーションして作成しました。
使用したプログラムは下の画像の通りです。
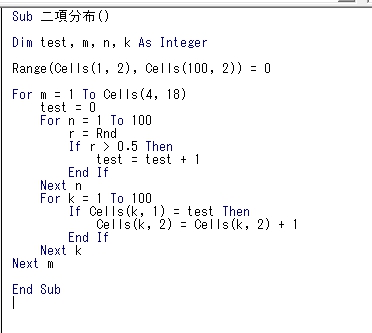
0から1までの値をランダムにとる乱数というものを使い、値が0.5より大きいなら1点追加、0.5以下なら点数はそのままとしています。
いずれこの乱数についてもブログで書きたいと思います。
それでは、どんどん実験する人数を増やしてみましょう。
今度は1000人に100回のカードめくりをやってもらいます。
下の画像のグラフができました。
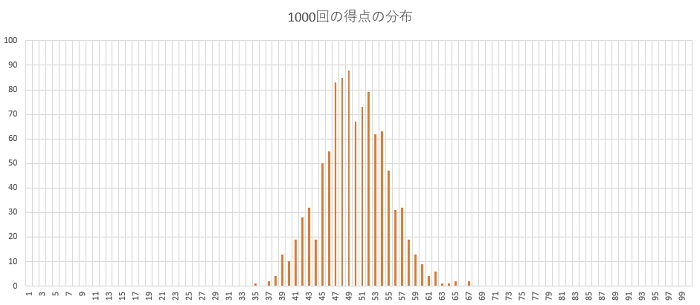
さらに数を増やしてみましょう。
今度は100000人に協力してもらいます。
現実世界では難しい実験でも、コンピューターに頼ればあっという間です。
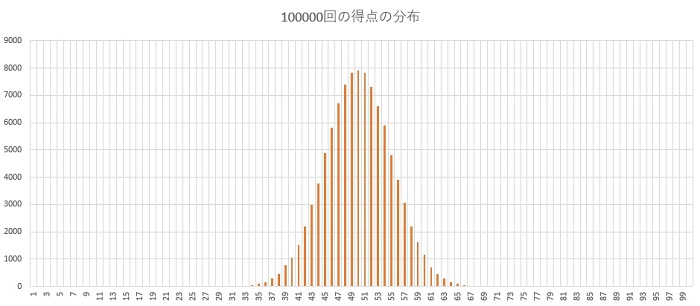
こうして見ると、100000回では左右対称に近い形になっています。
100回より1000回、1000回より100000回と試行の回数を増やすごとに、分布の形は左右対称な形になっていきます。
ところで、このような形に見覚えのある方がいらっしゃるかもしれません。
このページの冒頭で紹介した、偏差値についての記事に書かれていた、正規分布というものにそっくりな形をしています。
下の画像が正規分布の曲線です。
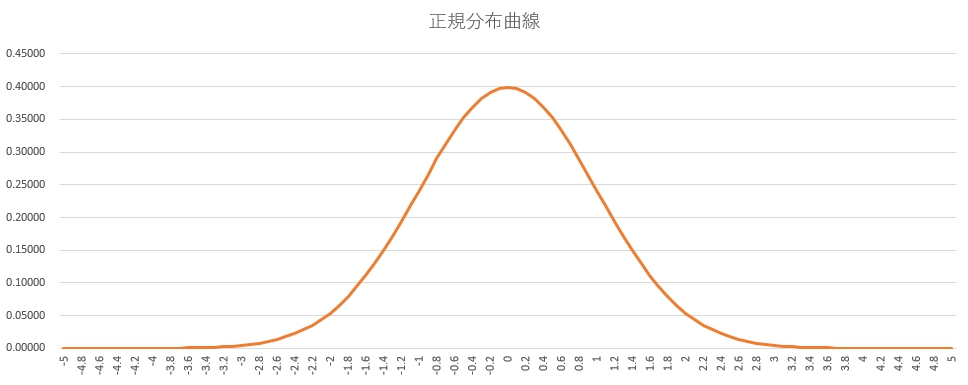
実は二項分布は、カードをめくる人数を増やしていくと正規分布に近づいていきます。
これをドゥ・モアブル=ラプラスの定理といいます。
さて、最後に二項分布の形の特徴について見ておきましょう。

この分布の特徴の1つ目は、50点付近に人数が固まっていることです。
また2つ目の特徴は、中心から外れると急激に人数が少なくなっていることです。
なぜこのような特徴を持つ形になるのでしょうか。
これについては理由を書かないので、下記の分布を作ったルールと照らし合わせ、ぜひ皆さんが考えてみてください。
1.点数がゼロからスタートします。
2.二枚のカードを裏返し、どちらがどちらか分からないよう、カードをよくシャッフルします。
3.どちらか一枚を表にします。
4.星が出たら点数に1点追加し、矢印の場合は点数が変わりません。
5.2~4を100回繰り返します。
高校生で数学Ⅱの二項定理を習った方はもうお分かりですね。
二項分布は高校の数学Ⅱで習う二項定理や、パスカルの三角形というものに大きく関わっています。
二項分布と正規分布の関係もそうですが、このように関係のあるもの同士を見つけたり、関連事項を考えたりすることは、数学や理科の力を大きく伸ばすきっかけになります。
学校の授業でも日常生活の中でも、何か共通なものがないかと常にアンテナを張ることが大事です。
意外なところに共通点があったりします。
例えばウツボとキリンとカエルの共通点とか...









