
教室ブログ
割り算と余りで数学のカーペットを作ろう!!
生徒・保護者・地域の皆様。
お世話になっております。
個別指導Wam城北中曽根校の小島です。
年始から続いた大雪はだいぶ前に治まりましたが、道の端には溶け残った雪が高く積もっています。
まだ寒い日が続く今日このごろ。
早く暖かくなってほしい・もう雪は降らないでほしいと切に願うばかりです。
さて、寒い時期には防寒用具がほしいところです。
そういうわけで、数学を使ってカーペットを作ってみましょう。
小学校で勉強する割り算と余りを利用します。
下の画像を御覧ください。
9つの部分に区切られたマス目があります。
色々と書いてあって目移りしますが、順番に説明します。

それぞれのマス目には番号が割り振られています。
例えば、一番左上のマスはm=1,n=1という番号が割り振られています。
真ん中はm=2,n=2という番号になっています。
真ん中から一つ右に行くと、m=2,n=3というマス目になります。
さて、一番左上のマス目に注目しましょう。
一番左上はm=1,n=1というマス目でした。
このmとnを足し算すると、m+n=1+1=2となります。
この2を3で割ってみましょう。
2÷3=0余り2
計算で出てきた余り2は、1よりも大きいです。
そこで、一番左上のm=1,n=1のマスを黒く塗ります(上の画像では文字が見えなくなるといけないので、灰色で塗りました)。
このようにして、
①それぞれのセルの番号mとnを足し算する
②その答えを3で割る
③その余りが1より大きいときはマス目を黒く塗る
という操作を行っていきます。
もう一つ計算してみましょう。
今度は一番右上のマス目で計算します。
m=1,n=3となるので、m+n=1+3=4
4÷3=1余り1
出てきた余りの1は、基準の数の1より大きくないので、このマス目は塗らずにそのままにしておきます。
このようにして全部のマス目で計算し、3で割って余りが1より大きいマス目を塗っていくと、下の画像のような模様になります。

ようやく模様が描けましたが、これだけではあまり面白くありません。
もっと大きいキャンバスを用意してみましょう。

100✕100のマス目を用意しました。
今度はこれを使って模様を描いていきます。
ただ、1マス1マス計算するのはとても大変です。
一枚仕上げるのに日が暮れてしまいます。
そこで、機械の力を借りることにしましょう。
このマス目はExcelというソフトを利用して作ったのですが、Excelにはプログラミングでマス目の操作をする機能が付いています。
命令を書くと、その通りにコンピューターが計算やマス目を塗る作業を行ってくれます。
ここから先は少しだけプログラミングの話が続きます。
興味の無い方は飛ばしてください。
実際に書いた命令が下の画像です。
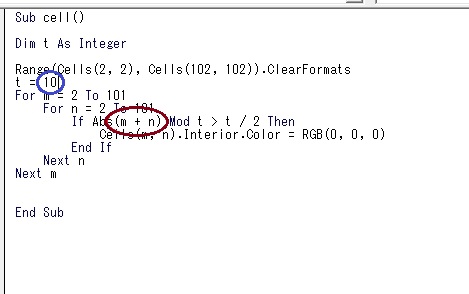
青で囲んだt=10というところが割る数を指定する部分です。
ここをt=3とすると、先程と同じく3で割った余りを求める計算をしてくれます。
赤で囲んだ部分が、mとnの計算方法を決める部分です。
今はm+nになっているので、先程と同じくmとnを足す計算式になっています。
さて、早速プログラムを動かしてみましょう。
m+nを10で割った余りが5より大きいマス目を黒く塗っていきます。
一番最初の模様をヒントに、どんな模様になるか予想してみてください。

こんな模様になりました。
予想は当たりましたか。
正直なところ、これでは斜めの線が何本も続いているだけで、まだあまり面白くありません。
もっと計算式を複雑にしてみましょう。
先程m+nとしていたところを、m^2+n^2としてみましょう。
「^2」は2乗と言って、同じ数を2回掛ける計算のことです。
m^2=m✕mとなります。
なのでこの式は、m✕m+n✕nという式を意味します。
プログラムのm+nをm^2+n^2に変え、カーペットを描いてみましょう。

とても複雑な模様ができあがりました。
複雑な中にもしっかりとした規則があり、とても美しい模様です。
小学校で習うわり算と余りから、こんなにも複雑な模様を描くことができました。
さて、式を複雑にしていけばどんどん複雑な模様が描けそうです。
割る数も色々と変えながら試してみましょう。
そうして色々と模様を作ってみて、完成したのが下の画像のカーペットです。
9つの模様をつなぎ合わせました。

これで寒い冬もバッチリです。









