
教室ブログ
皆さんこんにちは。個別指導Wam荻野校の星野です。
前回、数学の証明問題を得意にする方法を載せました。
そこで、「例えばどんな問題を覚えればいいの?」と、聞かれることがありました。
そりゃそうですよね^^;
ですので今回は「こんな問題を、こういう所をきっちり書けるように覚えて下さいね」という例題を出してみます。
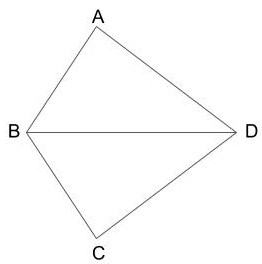
上の図で、AB=CB、BDは∠ABCの二等分線です。
この時、AD=CDとなる事を証明しなさい。
【証明】
△ABDと△CBDにおいて
仮定からAB=CB ‥①
∠ABD=∠CBD ‥②
また、BDは共通 ‥③
①、②、③より、二辺とその間の角がそれぞれ等しいから、
△ABD≡△CBD
合同な図形の辺は等しいから
AD=CD
こんな感じの基本問題です。
最初に教えるときは、結論がAD=CDだから、それらを含む三角形が、合同な三角形である事を示せばよく、そのための手がかりとして仮定の①~③を使おうという説明があるかと思います。
けれども、説明云々より、一言一句間違えずに覚えよう。そして、基本的な問題3~4問で、それができるようにしようというやり方でした。
ちょっと乱暴に思えますが、空手や剣道などでいう「型」にあたり、最初はなんでやっているか解らない所もあるかと思いますが、「習うより慣れろ」という事で、慣れたら「習う」の部分も後からついてくるという事です。
あくまで方法の一つで、証明問題を解く方法としてはもっと別な方法もあると思います。けれども私自身は、中学の時に同じように教わり、解けるようになりました。1つ参考にして頂ければ幸いです!









