
教室ブログ
こんにちは
個別指導Wam曽野木校の小島です。
前回は、中学3年生までの知識を使い、
黄金長方形から黄金比1:1.618を導出しました。
今回は、高校の数学Bで習う漸化式を使い、
フィボナッチ数列というものから黄金比を導出してみます。
高校数学の知識が出てきますし、式変形は難しくなりますが、できるだけわかりやすく書きます。
今回も前回と同じく厳密な話ではありません。
さて、準備のために高校で習う数列について話しておきましょう。
数列というのは、例えば、
1 , 2 , 3 , 4 , 5 , … ①
2 , 4 , 6 , 8 , 10 , … ②
-10 , -20 , -35 , 51 , 1024 , … ③
というように数を一列に並べたもののことです。
ここで問題。
上の数列はどういう数字の並びになっているでしょうか。
正解は下のほうにスクロールすると書いてあります。
正解は、
①は自然数を並べたもの
②は偶数を並べたもの
③は思いついた数をてきとうに並べたものです
みなさん正解できたでしょうか。
さて、冒頭でお話したフィボナッチ数列について説明していきます。
フィボナッチ数列というのは、1からスタートして、
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , …
という並びの数列です。
この数列はどういう規則になっているでしょうか。
正解は下に書いてあります。
フィボナッチ数列の規則は、2つ前と1つ前の数字を足すと、その次の数字になるというものです。
例えば、最初の1と次の1を足すと、その次の2になっています( 1 + 1 = 2 )。
また、5番目の5と6番目の8を足すと、7番目の13になっています( 5 + 8 = 13 )。
このように、並んでいる2つの数字を足すと、次の数字になっています。
これを高校で習う漸化式で表すと、
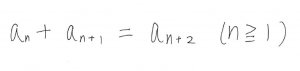
となります。
nは1番目とか3番目とか、何番目かを表す数字です。
この数式は、n番目とn+1番目の数字を足すと、n+2番目の数字になるという意味で、
4番目と5番目の数字を足すと6番目の数字になるとか、
105番目と106番目の数字を足すと107番目の数字になるとかを、
まとめて一つの式で表しています。
数式で表すといきなり難しくなった気がしますが、
そんなものなんだなあ、ぐらいに思ってもらえれば大丈夫です。
例えば、a1は一番目の数を表していて、
フィボナッチ数列であればa1 = 1です。
同様にフィボナッチ数列で考えると、
a2 = 1
a3 = 2
a4 = 3
a5 = 5
ですし、
a2 + a3 = 1 + 2 = 3 = a4
となります。
さて、ここからこの式を変形していくので、話が少し難しくなります。
数学が苦手な方は、計算を飛ばして結論だけご覧ください。
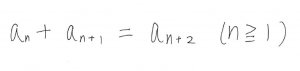
この式の左辺と右辺を入れ替え、anとan+1の順番も入れ替えておきます。
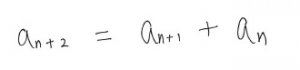
そうしたら、両辺をan+1で割ってみましょう。
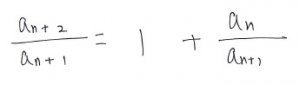
このとき、左辺は次の数と前の数の比になっていることに注意して下さい。
ここで、an+1 = an + an-1 なので、右辺の an+1 に代入すると、
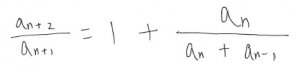
となります。右辺の分数の分子と分母をanで割ってみましょう。すると、
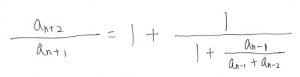
となりました。
前にan+1 = an + an-1 を an+1 に代入したように、
今度はanに an = an-1 + an-2
を代入してみましょう。
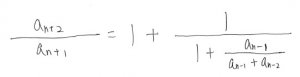
このように、代入して割ってを繰り返していきます。
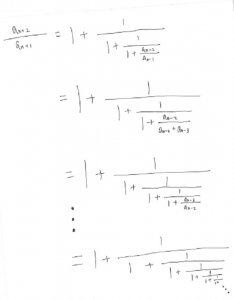
ここで左辺の比をxと置いておきます。
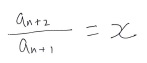
すると、
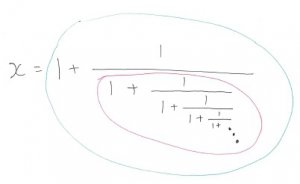
上の式の赤丸部分と緑丸部分を比べてみてください。
よく見ると、どちらも同じ形をしています。
ここで、右下の点の部分が無限に続いていくと考えると、
赤丸部分と緑丸部分は等しくなります。緑丸はxと等しいので、
緑丸 = 赤丸 = x
となり、上の式は
![]()
となります。どこかで見た形の式です。
そう、これは前回の黄金長方形から導出した2次方程式と同じものです。
これを解くと、
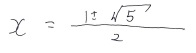
となって、+の方の解が1.618…となるのでした。
さて、長くかかりましたが、これで黄金比の導出は終わりです。
ここまで見ていただいて有難うございました。









