
教室ブログ
こんにちは。
個別指導Wam曽野木校の小島です。
今回は、中学3年生で習う2次方程式の知識を使い、1:1.618という数字の起源をさぐってみましょう。
なお、今回の話の中には数学的な厳密性を欠いている部分があります。
あらかじめご了承ください。
スタートは、前回お話した黄金長方形です。
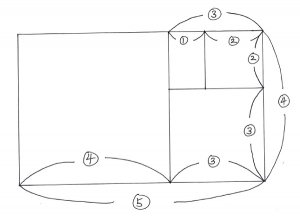
長方形の辺にそれぞれ番号を振ってみました。
上の画像の通り、この辺には
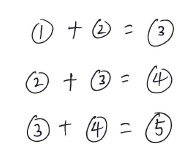
という関係が成り立っています。
ここで、連続した番号の辺同士の比がどれも同じになると仮定して、その比をxとおいてみましょう。
つまりこういうことです。
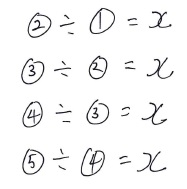
長いほうを短いほうで割ると、どれもxという値になると仮定します。
さて、この辺の比の関係から、
①=1
とすると、
②=x
③=(xの2乗)
となります。
一番目と二番目の辺の長さを足すと、三番目の辺の長さになるという関係(①+②=③)と合わせて、下の式のようにxを求めることができます。
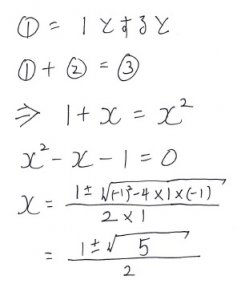
辺同士の比xは、どうやら無理数になるようです。
この値がどのくらいになるのか、電卓で計算してみましょう。
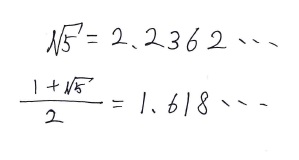
というわけで、1.618という値を導出することができました。
次回は、高校で習う漸化式と極限を用いて、1.618を導出してみましょう。









